In this chapter, we would like to remind you the concepts of countable and uncountable sets, as well as the general techniques involved in countability and uncountability proofs. Even though it may seem like we are diverging from the main discussion on computation, we’ll see in future chapters that the concepts in this chapter are intimately related to the concepts of computability and uncomputability. Countable and uncountable sets, together with the diagonalization proof technique, have major applications in proving the limits of computation.
Let \(X\) and \(Y\) be two (possibly infinite) sets.
A function \(f: X \to Y\) is called injective if for any \(x,x' \in X\) such that \(x \neq x'\), we have \(f(x) \neq f(x')\). We write \(X \hookrightarrow Y\) if there exists an injective function from \(X\) to \(Y\).
A function \(f: X \to Y\) is called surjective if for all \(y \in Y\), there exists an \(x \in X\) such that \(f(x) = y\). We write \(X \twoheadrightarrow Y\) if there exists a surjective function from \(X\) to \(Y\).
A function \(f: X \to Y\) is called bijective (or one-to-one correspondence) if it is both injective and surjective. We write \(X \leftrightarrow Y\) if there exists a bijective function from \(X\) to \(Y\).
Let \(X, Y\) and \(Z\) be three (possibly infinite) sets. Then,
\(X \hookrightarrow Y\) if and only if \(Y \twoheadrightarrow X\);
if \(X \hookrightarrow Y\) and \(Y \hookrightarrow Z\), then \(X \hookrightarrow Z\);
\(X \leftrightarrow Y\) if and only if \(X \hookrightarrow Y\) and \(Y \hookrightarrow X\).
Let \(X\) and \(Y\) be two sets.
We write \(|X| = |Y|\) if \(X \leftrightarrow Y\).
We write \(|X| \leq |Y|\) (or \(|Y| \geq |X|\)) if \(X \hookrightarrow Y\), or equivalently, if \(Y \twoheadrightarrow X\).
We write \(|X| < |Y|\) (or \(|Y| > |X|\)) if it is not the case that \(|X| \geq |Y|\).
Theorem (Relationships between different types of functions) justifies the use of the notation \(=\), \(\leq\), \(\geq\), \(<\) and \(>\). The properties we would expect to hold for this type of notation indeed do hold. For example,
\(|X| = |Y|\) if and only if \(|X| \leq |Y|\) and \(|Y| \leq |X|\),
if \(|X| \leq |Y| \leq |Z|\), then \(|X| \leq |Z|\),
if \(|X| \leq |Y| < |Z|\), then \(|X| < |Z|\), and so on.
If \(X \subseteq Y\), then \(|X| \leq |Y|\) since the identity function that maps \(x \in X\) to \(x \in Y\) is an injection.
Let \(\mathbb S= \{0, 1, 4, 9,\ldots\}\) be the set of squares. Then \(|\mathbb S| = |\mathbb N|\).
The function \(f : \mathbb N\to \mathbb S\) defined as \(f(n) = n^2\) is a bijection. It is an injection since if \(n^2 = m^2\), then \(n = m\). And it is surjective since for every \(s \in \mathbb S\), by the definition of \(\mathbb S\), there exists an \(n\) such that \(n^2 = s\).
Let \(\mathbb Z\) be the set of integers. Then \(|\mathbb Z| = |\mathbb N|\).
Since \(\mathbb N\subseteq \mathbb Z\), we have \(|\mathbb N| \leq |\mathbb Z|\). So we just need to argue \(|\mathbb Z| \leq |\mathbb N|\), i.e. there is a surjective function \(f\) from \(\mathbb N\) to \(\mathbb Z\). For this, our strategy is to argue that we can list the elements of \(\mathbb Z\) such that every element eventually appears in the list. If we can do this, then we have the surjection \(f\) that we want: we let \(f(n)\) be the \(n\)’th element in the list. Creating such a listing of \(\mathbb Z\) is relatively straightforward: \[0, \; 1, \; -1, \; 2, \; -2, \; 3, \; -3, \; \ldots\] With this listing, the mapping \(f\) is such that odd numbers are mapped to positive integers and even numbers are mapped to non-positive integers. The formula for \(f\) is \[f(n) = \begin{cases} -n/2 & \text{ if $n$ is even,} \\ (n+1)/2 & \text{ if $n$ is odd.} \end{cases}\]
Let \(\mathbb Z\times \mathbb Z\) be the set of tuples with integer coordinates. Then \(|\mathbb Z\times \mathbb Z| = |\mathbb N|\).
We will show \(|\mathbb Z\times \mathbb Z| = |\mathbb N|\) by arguing \(|\mathbb N| \leq |\mathbb Z\times \mathbb Z|\) and \(|\mathbb Z\times \mathbb Z| \leq |\mathbb N|.\)
The former doesn’t really require much of an argument. The map \(n \mapsto (n,0)\) is an injection and so \(|\mathbb N| \leq |\mathbb Z\times \mathbb Z|.\)
For the latter, we will show that there is a surjective function \(f\) from \(\mathbb N\) to \(\mathbb Z\times \mathbb Z\), and we will do so by arguing that we can list the elements of \(\mathbb Z\times \mathbb Z\) such that every element eventually appears in the list. If we can do this, then we have the surjection \(f\) that we want: we let \(f(n)\) be the \(n\)’th element in the list.
We now describe how to list the elements of \(\mathbb Z\times \mathbb Z\). Consider the plot of \(\mathbb Z\times \mathbb Z\) on a 2-dimensional grid. Starting at \((0,0)\) we list the elements of \(\mathbb Z\times \mathbb Z\) using a spiral shape, as shown below.
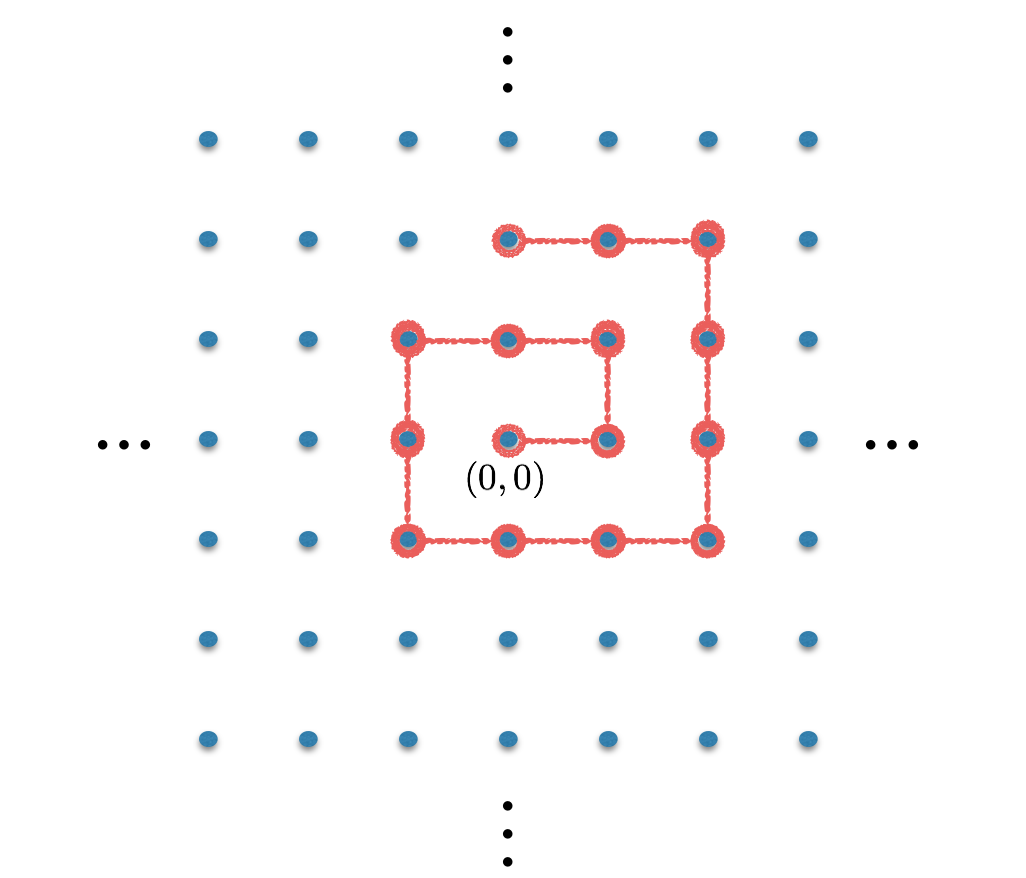
(The picture shows only a small part of the spiral.) Since we have a way to list all the elements such that every element eventually appears in the list, we are done.
(Side node: It is not a requirement that we give an explicit formula for \(f(i)\). In fact, sometimes in such proofs, an explicit formula may not exist. This does not make the proof any less rigorous! The above proof is perfectly acceptable.)
Let \(\mathbb Q\) be the set of rational numbers. Then \(|\mathbb Q| = |\mathbb N|\).
We want to show \(|\mathbb Q| = |\mathbb N|\), and it is clear that \(|\mathbb N| \leq |\mathbb Q|\) (since \(\mathbb N\subseteq \mathbb Q\)), so we just need to show \(|\mathbb Q| \leq |\mathbb N|\). We will make use of the previous proposition to establish this.
Note that every element of \(\mathbb Q\) can be written as a fraction \(a/b\) where \(a, b \in \mathbb Z\). In other words, there is a surjection from \(\mathbb Z\times \mathbb Z\) to \(\mathbb Q\) that maps \((a,b)\) to \(a/b\) (if \(b = 0\), map \((a,b)\) to say \(0\)). This shows that \(|\mathbb Q| \leq |\mathbb Z\times \mathbb Z|\). From the previous proposition, \(|\mathbb Z\times \mathbb Z| = |\mathbb N|\). Putting things together, \(|\mathbb Q| \leq |\mathbb N|\).
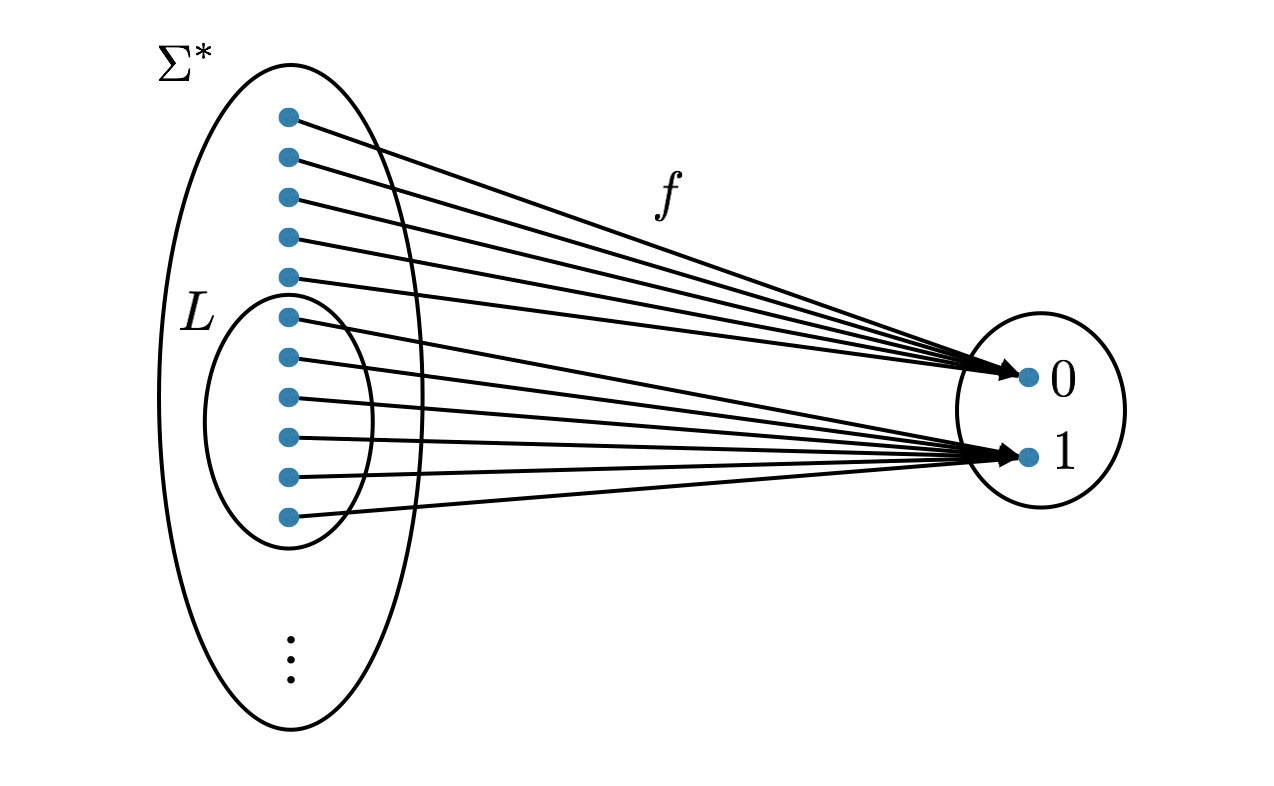
Let \(\Sigma\) be a finite non-empty set. Then \(|\Sigma^*| = |\mathbb N|\).
Recall that \(\Sigma^*\) denotes the set of all words/strings over the alphabet \(\Sigma\) with finitely many symbols. We want to show \(|\mathbb N| \leq |\Sigma^*|\) and \(|\Sigma^*| \leq |\mathbb N|\).
To show \(|\mathbb N| \leq |\Sigma^*|\), note that the function that maps a string to its length, \(s \mapsto |s|\), is a surjection from \(\Sigma^*\) to \(\mathbb N\). (Remark: When \(|\Sigma| = 1\), this function is a bijection.)
We will now show \(|\Sigma^*| \leq |\mathbb N|\) by presenting a way to list all the elements of \(\Sigma^*\) such that eventually all the elements appear in the list. (As before, if we can present this listing, then we have a surjection \(f : \mathbb N\to \Sigma^*\): we let \(f(n)\) be the \(n\)’th element in the list.)
For each \(k = 0,1,2,\ldots\), let \(\Sigma^k\) denote the set of words in \(\Sigma^*\) that have length exactly \(k\). Note that \(\Sigma^k\) is a finite set for each \(k\), and \(\Sigma^*\) is a union of these sets: \(\Sigma^* = \Sigma^0 \cup \Sigma^1 \cup \Sigma^2 \cup \cdots\). This gives us a way to list the elements of \(\Sigma^*\) so that any element of \(\Sigma^*\) eventually appears in the list. First list the elements of \(\Sigma^0\), then list the elements of \(\Sigma^1\), then list the elements of \(\Sigma^2\), and so on.
If \(S\) is an infinite set and \(|S| \leq |\mathbb N|\), then \(|S| = |\mathbb N|\).
Prove the above theorem.
Assume \(S\) is such that \(|S| \leq |\mathbb N|\) and \(S\) is infinite. Since \(|S| \leq |\mathbb N|\), there is an injection \(f : S \to \mathbb N\). This \(f\) allows us to define an ordering on \(S\). For \(s, t \in S\), write \(s < t\) if \(f(s) < f(t)\). Using this ordering, we can define the order of an element \(s \in S\) as \(\text{ord}(s) = |\{x \in S : f(x) < f(s)\}|\).
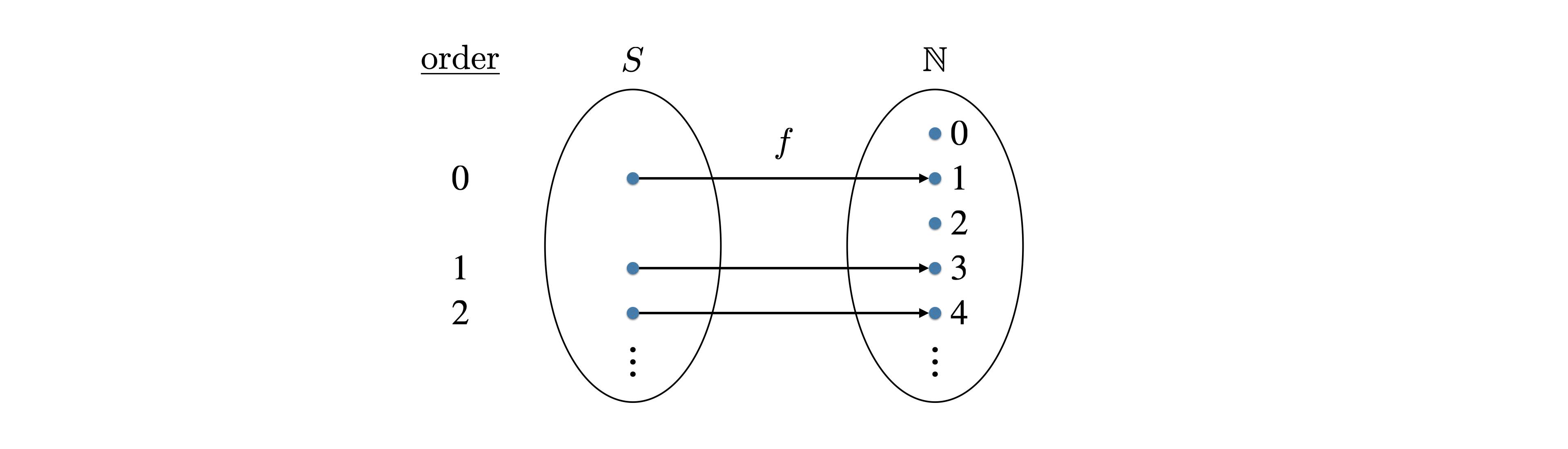
We now observe that the \(\text{ord}\) function that we have defined is a bijection from \(S\) to \(\mathbb N\). To see that this is a bijection, first note that it is a surjective function because \(S\) is an infinite set. And it is an injective function because it is a total order. In particular, if \(\text{ord}(s) = \text{ord}(s')\), then it must be \(f(s) = f(s')\), and since \(f\) is injective, this implies \(s = s'\).
Let \(\mathbb{P} = \{2, 3, 5, 7, \ldots\}\) be the set of prime numbers. Then \(|\mathbb{P}| = |\mathbb N|\).
Since \(\mathbb{P} \subseteq \mathbb N\), we know \(|\mathbb{P}| \leq |\mathbb N|\). We also know that there are infinitely many primes. Then by Theorem (No cardinality strictly between finite and \(|\mathbb N|\)), \(|\mathbb{P}| = |\mathbb N|\).
(One can also prove this proposition without invoking the theorem. The function that maps \(n\) to the \(n\)’th prime number is a bijection.)
In the last section, we have shown \(|\mathbb N| = |\mathbb S| = |\mathbb Z| = |\mathbb{P}| = |\mathbb Z\times \mathbb Z| = |\mathbb Q| = |\Sigma^*|.\) In light of Theorem (No cardinality strictly between finite and \(|\mathbb N|\)), there are three categories of sets:
finite sets,
sets \(S\) such that \(|S| = |X|\), where \(X\) is any of the sets listed above (like \(\mathbb N\)),
all other sets (i.e. sets \(S\) with \(|S| > |X|\), where \(X\) is any of the sets listed above).
It makes sense to give a name for these different categories. In the literature, the first two categories combined is known as countable sets. And the third category is known as uncountable sets.
We can define a countable set as any set \(S\) with \(|S| \leq |X|\), where \(X = \mathbb N\). But the choice of \(\mathbb N\) here, in a sense, is arbitrary. We can also choose, for instance, \(X = \Sigma^*\), in which case we see countability is equivalent to encodability. And arguably, encodability captures the essence of this class of sets better. That being said, in the literature, \(X = \mathbb N\) is the standard choice, leading to the definition below.
A set \(S\) is called countable if \(|S| \leq |\mathbb N|\).
A set \(S\) is called countably infinite if it is countable and infinite.
A set \(S\) is called uncountable if it is not countable, i.e. \(|S| > |\mathbb N|\).
Theorem (No cardinality strictly between finite and \(|\mathbb N|\)) implies that if \(S\) is countable, there are two options: either \(S\) is finite, or \(|S| = |\mathbb N|\).
Recall that a set \(S\) is encodable if for some alphabet \(\Sigma\), there is an injection from \(S\) to \(\Sigma^*\), or equivalently, \(|S| \leq |\Sigma^*|\) (Definition (Encoding elements of a set)). Since \(|\mathbb N| = |\Sigma^*|\), we see that a set is countable if and only if it is encodable. Therefore, one can show that a set is countable by showing that it is encodable. We will call this the “CS method” for showing countability.
The standard definition of countability (\(|S| \leq |\mathbb N|\)) highlights the following heuristic.
If you can list the elements of \(S\) in a way that every element appears in the list eventually, then \(S\) is countable.
The encodability definition highlights another heuristic that is far more relevant in computer science.
If you can “write down” each element of \(S\) using a finite number of symbols, then \(S\) is countable.
The set of all polynomials in one variable with rational coefficients is countable.
Let \(\mathbb Q[x]\) denote the set of all polynomials in one variable with rational coefficients. We want to show that \(\mathbb Q[x]\) is countable. We will do so using the CS method. Let \[\Sigma = \{{\texttt{0}},{\texttt{1}},{\texttt{2}},{\texttt{3}},{\texttt{4}},{\texttt{5}},{\texttt{6}},{\texttt{7}},{\texttt{8}},{\texttt{9}},{\texttt{+}},{\texttt{-}},{\texttt{/}},{\texttt{x}}\}.\] Then observe that every element of \(\mathbb Q[x]\) can be written as a finite string over this alphabet. For example, \[{\texttt{2x3-1/34x2+99/100x1+22/7}}\] represents the polynomial \[2x^3 - 1/34x^2 + 99/100x + 22/7.\] This implies that there is a surjective map from \(\Sigma^*\) to \(\mathbb Q[x]\). And therefore \(|\mathbb Q[x]| \leq |\Sigma^*|\). Since \(\Sigma^*\) is countable, i.e. \(|\Sigma^*| \leq |\mathbb N|\), \(\mathbb Q[x]\) is also countable.
Show that the following sets are countable.
\(\mathbb Z\times \mathbb Z\times \mathbb Z\).
The set of all functions \(f: S \to \mathbb N\), where \(S\) is some fixed finite set.
Part 1: We want to show that \(\mathbb Z\times \mathbb Z\times \mathbb Z\) is countable. We use the CS method with \(\Sigma = \{{\texttt{0}},{\texttt{1}},{\texttt{2}},{\texttt{3}},{\texttt{4}},{\texttt{5}},{\texttt{6}},{\texttt{7}},{\texttt{8}},{\texttt{9}},{\texttt{-}},{\texttt{\$}}\}\). Note that any element of \(\mathbb Z\times \mathbb Z\times \mathbb Z\) can be written uniquely as a finite word over \(\Sigma\) (we use the dollar sign as a separator between the integers). As an illustration, \((9234851,\text{-}1234,0) \in \mathbb Z\times \mathbb Z\times \mathbb Z\) can be encoded as the string \({\texttt{9234851\$-1234\$0}}\). Every integer has finite length, so the string encoding is always of finite length.
Part 2: Let \(U\) be the set of all functions \(f: S \to \mathbb N\), where \(S\) is a finite set. We want to show that \(U\) is countable.
We first make an observation about the elements of \(U\). Take a function \(f: S \to \mathbb N\), where \(S\) is a finite set. Let \(k\) be the size of \(S\) and let \(s_1, s_2, \ldots, s_k\) be its elements. Then \(f\) can be uniquely represented by the tuple \[(f(s_1), f(s_2), \ldots, f(s_k)),\] where each element of the tuple is an element from \(\mathbb N\).
We now show that \(U\) is countable using the CS method with the alphabet \(\Sigma = \{{\texttt{0}},{\texttt{1}},{\texttt{2}},{\texttt{3}},{\texttt{4}},{\texttt{5}},{\texttt{6}},{\texttt{7}},{\texttt{8}},{\texttt{9}},{\texttt{\$}}\}\). The observation above shows that any element of \(U\) can be uniquely represented with a finite length string where commas are replaced with \({\texttt{\$}}\). (Note that there is no need to put the opening and closing parentheses.) This suffices to conclude that \(U\) is countable.
Let \(\mathcal{F}\) be a set of functions \(f: X \to Y\) where \(|Y| \geq 2\). If \(|X| \geq |\mathcal{F}|\), we can construct a function \(f_D : X \to Y\) such that \(f_D \not \in \mathcal{F}\).
Given a set \(\mathcal{F}\) of functions \(f: X \to Y\), we want to construct a function \(f_D : X \to Y\) that is different from every \(f \in \mathcal{F}\). The main idea is the following. For each \(f \in \mathcal{F}\), pick a unique input \(x \in X\) and define \(f_D(x)\) in a way such that it is different from \(f(x)\). Since by construction \(f_D\) and \(f\) disagree on input \(x\), \(f_D\) is different from \(f\). And since we do this for every \(f \in \mathcal{F}\), \(f_D\) is different from all \(f \in \mathcal{F}\).
Above, it is important that we pick a unique \(x\) for each \(f \in \mathcal{F}\) so that \(f_D\) can be defined in a consistent way. The ability to pick a unique \(x\) for each \(f \in \mathcal{F}\) is equivalent to \(|X| \geq |\mathcal{F}|\).
A bit more formally, since \(|X| \geq |\mathcal{F}|\), there is an injection \(\phi : \mathcal{F}\to X\). Let \(x_f = \phi(f)\). So \(f \neq f'\) implies \(x_f \neq x_{f'}\). Define \(f_D\) such that for all \(f \in \mathcal{F}\), \(f_D(x_f) \neq f(x_f)\) (this is where the assumption \(|Y| \geq 2\) is used). This ensures that \(f_D\) is different from every \(f \in \mathcal{F}\), and therefore \(f_D \not \in \mathcal{F}\). (Note that our description of \(f_D\) leaves it underspecified, but see the remark below.)
When we apply the above lemma to construct an explicit \(f_D \not\in \mathcal{F}\), we call that diagonalizing against the set \(\mathcal{F}\). And we call \(f_D\) a diagonal element. Typically there are several choices for the definition of \(f_D\):
Different injections \(\phi : \mathcal{F}\to X\) can lead to different diagonal elements.
If \(|Y| > 2\), we have more than one choice on what value we assign to \(f_D(x_f)\) that makes \(f_D(x_f) \neq f(x_f)\) (here \(x_f\) denotes \(\phi(f)\)).
If there are elements \(x \in X\) not in the range of \(\phi\), then we can define \(f_D(x)\) any way we like.
Many mathematical objects can be easily viewed as functions. The following are some examples.
A set \(S \subseteq U\) can be viewed as a function \(f_S: U \to \{0,1\}\). This is called the characteristic function of the set. Recall that we made this observation in Important Note (Correspondence between decision problems and languages).
A sequence \(s\) of length \(k\) with elements from a set \(Y\) can be viewed as a function \(f_s : \{1,2,\ldots,k\} \to Y\), where \(f_s(i)\) is the \(i\)’th element of the sequence.
A string/word is a sequence of symbols from an alphabet \(\Sigma\). Therefore a string \(s \in \Sigma^*\) with \(|s| = k\) can be viewed as a function \(f_s : \{1,2,\ldots,k\} \to \Sigma\).
An infinite-length sequence \(s\) with elements from \(Y\) can be viewed as a function \(f_s : \mathbb N^+ \to Y\).
Numbers can be viewed as functions since the binary representation of a number is just a string/sequence of bits (possibly infinite-length).
Note that diagonalizing against a set \(\mathcal{F}\) produces an explicit function \(f_D\) not in \(\mathcal{F}\). Therefore, in situations where you wish to find an explicit object that is not in a given set, you should consider if diagonalization could be applied.
If \(\mathcal{F}\) is the set of all functions \(f: X \to Y\) (and \(|Y| \geq 2\)), then \(|X| < |\mathcal{F}|\).
Diagonalization tells us that whenever \(|X| \geq |\mathcal{F}|\), we can construct a function \(f_D\) not in \(\mathcal{F}\). But if \(\mathcal{F}\) denotes the set of all functions \(f: X \to Y\), the construction of \(f_D\) is not possible. Therefore it must be the case that \(|X| < |\mathcal{F}|\).
Let \(\mathcal{F}\) be the set of all functions \(f : X \to \{0,1\}\), which are the characteristic functions of the subsets of \(X\) (so \(f(x) = 1\) if and only if \(x \in X\)). Then by Note (Functions in disguise), \(|\mathcal{F}| = |\wp(X)|\) and the result follows from the above Corollary.
In the famous Russell’s Paradox, we consider the set of all sets that do not contain themselves. That is, we consider \[D = \{\text{set } S : S \not \in S\}.\] Then we ask whether \(D\) is in \(D\) or not. If \(D \in D\), then by the definition of \(D\), \(D \not \in D\). And if \(D \not \in D\), again by the definition of \(D\), \(D \in D\). Either way we get a contradiction. Therefore, the conclusion is that such a set \(D\) should not be mathematically definable.
This paradox is also an application of diagonalization. For any set \(X\), we cannot diagonalize against the set of all functions \(f : X \to \{0,1\}\). If we imagine diagonalizing against this set, where \(X\) is the set of all sets, the natural diagonal element \(f_D\) that comes out of diagonalization is precisely the characteristic function of the set \(D\) defined above.
For any infinite set \(S\), \(\wp(S)\) is uncountable. In particular, \(\wp(\mathbb N)\) is uncountable.
Let’s break this up into two cases: (i) \(S\) is countably infinite and (ii) \(S\) is uncountable.
If \(S\) is countably infinite, \(|S| = |\mathbb N|\). And by Cantor’s Theorem, \(|\mathbb N| = |S| < |\wp(S)|\), which by definition means \(\wp(S)\) is uncountable.
If \(S\) is uncountable, then \(|\mathbb N| < |S| < |\wp(S)|\), and so once again, \(\wp(S)\) is uncountable.
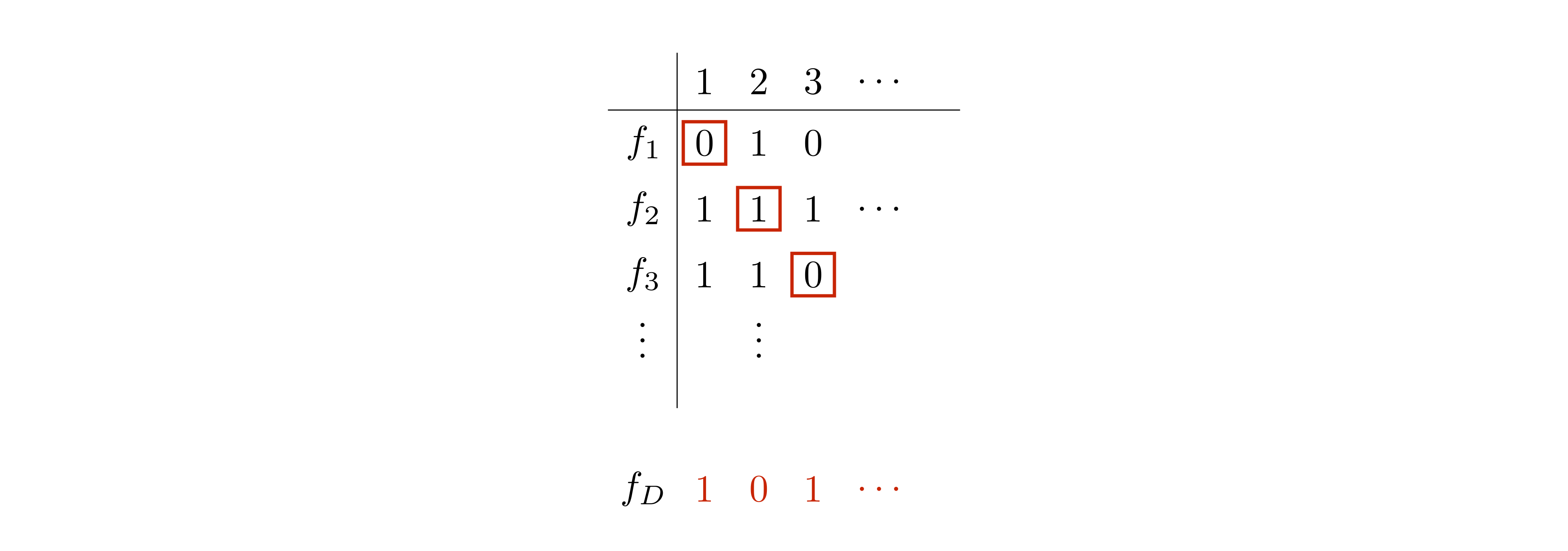
In a common scenario where diagonalization is applied, both \(\mathcal{F}\) and \(X\) are countably infinite sets. So we can list the elements of \(\mathcal{F}\) as \[f_1,\; f_2,\; f_3,\; \ldots\] as well as the elements of \(X\) as \[x_1,\; x_2,\; x_3,\; \ldots\] Then for all \(i\), define \(f_D(x_i)\) such that \(f_D(x_i) \neq f_i(x_i)\). If \(Y = \{0,1\}\), for example, \(f_D(x_i) = \textbf{not} \; f_i(x_i)\). The construction of \(f_D\) can be nicely visualized with a table, as shown below. Here, an entry corresponding to row \(f_i\) and column \(x_j\) contains the value \(f_i(x_j)\).

By construction, the diagonal element \(f_D\) differs from every \(f_i\), \(i \in \{1,2,3,\ldots\}\). In particular, it differs from \(f_i\) with respect to the input \(x_i\).
Below, we will apply Lemma (Diagonalization) to construct an irrational number (i.e. a number in \(\mathbb R\setminus \mathbb Q\)). Even though the result may not be interesting (since there is a relatively simple proof that \(\sqrt{2}\) is irrational), it does illustrate the use of diagonalization nicely. Cantor used the same technique to construct an explicit transcendental number, which was a quite non-trivial and important result at the time. Instead of proving that result, we put it in the practice set for you.
There exists an irrational real number, that is, there exists a number in \(\mathbb R\setminus \mathbb Q\).
We will prove the existence of a number in \(\mathbb R\setminus \mathbb Q\) (i.e. the existence of an irrational number) by constructing such a number using diagonalization. In order to simplify the proof, we will restrict our attention to numbers in the interval \([0,1]\), so we will construct an irrational number in \([0,1]\). The restriction to \([0,1]\) allows us to represent a number just by considering the fractional part.
As mentioned in Note (Functions in disguise), numbers can be viewed as functions: Every function \(f : \mathbb N^+ \to \{0,1\}\) represents a real number in \([0,1]\) in binary, namely \(0.f(1)f(2)f(3)\ldots\). Two different functions \(f\) and \(f'\) may represent the same real number, e.g. \(0.10000\ldots\) and \(0.01111\ldots\) represent the same real number. But we don’t have more than two different functions representing the same number.
Now consider the set \(\mathcal{F}\) of all functions \(f : \mathbb N^+ \to \{0,1\}\) representing a rational number. We will diagonalize against \(\mathcal{F}\) to construct \(f_D\) not in \(\mathcal{F}\). This \(f_D\) then represents a real number that is not rational, and we are done.
In order to diagonalize against \(\mathcal{F}\), all we need is that \(|\mathbb N^+| \geq |\mathcal{F}|\) holds. And this is indeed the case. \(\mathcal{F}\) is countably infinite because \(\mathbb Q\) is countably infinite. And obviously \(\mathbb N^+\) is countably infinite. This means we are in the situation outlined in Note (Diagonalization with countable sets), and \(|\mathbb N^+| = |\mathcal{F}|\).
The proof is basically the same as the proof of Proposition (Irrational numbers exist). There, we have implicitly proved that the interval \([0,1]\) cannot be countable. To see this, note that if \([0,1]\) is countable, then the set \(\mathcal{F}\) of all functions \(f : \mathbb N^+ \to \{0,1\}\) is countable. So \(|\mathcal{F}| = |\mathbb N^+|\), which allows us to diagonalize against \(\mathcal{F}\), which is not possible.
Let \(\Sigma\) be some finite alphabet. We denote by \(\Sigma^\infty\) the set of all infinite length words over the alphabet \(\Sigma\).
Observe that \(\Sigma^* \cap \Sigma^\infty = \varnothing\).
The set \(\{{\texttt{0}},{\texttt{1}}\}^\infty\) is uncountable.
Using the observation in Note (Functions in disguise), an infinite-length string \(s \in \{{\texttt{0}},{\texttt{1}}\}^\infty\) corresponds to a function \(f_s : \mathbb N^+ \to \{{\texttt{0}}, {\texttt{1}}\}\), which is the characteristic function of a set \(S \subseteq \mathbb N^+\) (where \(n \in S\) if and only if \(f_s(n) = {\texttt{1}}\)). Therefore the set of all infinite-length strings, \(\{{\texttt{0}},{\texttt{1}}\}^\infty\), corresponds to the set of all subsets of \(\mathbb N^+\), \(\wp(\mathbb N^+)\). That is, \(\{{\texttt{0}},{\texttt{1}}\}^\infty \leftrightarrow\wp(\mathbb N^+)\). Using Corollary (The power set of an infinite set is uncountable) we can conclude \(\{{\texttt{0}},{\texttt{1}}\}^\infty\) is uncountable.
Prove that if \(X\) is uncountable and \(X \subseteq Y\), then \(Y\) is also uncountable.
We want to show that if \(Y\) is a superset of an uncountable set \(X\), then \(Y\) must be uncountable.
If \(X\) is uncountable, by definition, \(|X| > |\mathbb N|\). If \(X \subseteq Y\), then there is a clear injection from \(X\) to \(Y\) (map \(x \in X\) to \(x \in Y\)), so \(|X| \leq |Y|\). Combining this with \(|X| > |\mathbb N|\), we have \(|Y| \geq |X| > |\mathbb N|\), and therefore \(Y\) is uncountable.
If we want to show that a set \(X\) is uncountable, it suffices to show that \(|X| \geq |Y|\) for some uncountable set \(Y\). Typically, a good choice for such a \(Y\) is \(\{{\texttt{0}},{\texttt{1}}\}^\infty\). And one strategy for establishing \(|X| \geq |\{{\texttt{0}},{\texttt{1}}\}^\infty|\) is to identify a subset \(S\) of \(X\) such that \(S \leftrightarrow\{{\texttt{0}},{\texttt{1}}\}^\infty\).
Show that the following sets are uncountable.
The set of all bijective functions from \(\mathbb N\) to \(\mathbb N\).
\(\{x_1x_2 x_3 \ldots \in \{{\texttt{1}},{\texttt{2}}\}^\infty : \text{ for all $n \geq 1$, $\; \sum_{i=1}^n x_i \not\equiv 0 \mod 4$}\}\)
Part 1: Let \(S\) be the set of all bijective functions from \(\mathbb N\) to \(\mathbb N\). We want to show that \(S\) is uncountable, and we will do so by showing that \(\{{\texttt{0}},{\texttt{1}}\}^\infty \hookrightarrow S\), establishing \(|\{{\texttt{0}},{\texttt{1}}\}^\infty| \leq |S|\).
We now describe this injective mapping. Given \(x \in \{{\texttt{0}},{\texttt{1}}\}^\infty\), we map it to a bijection \(f_x :\mathbb N\to \mathbb N\) as follows. Let \(x_n\) be the \(n\)’th bit of \(x\), and assume the indexing starts from \(0\). Then for all \(n \in \mathbb N\), \[\begin{aligned} \text{if $x_n = {\texttt{0}}$}, & \quad \text{$f_x$ maps $2n$ to $2n$ and $2n+1$ to $2n+1$;} \\ \text{if $x_n = {\texttt{1}}$}, & \quad \text{$f_x$ maps $2n$ to $2n+1$ and $2n+1$ to $2n$.}\end{aligned}\]
The below picture illustrates the construction of \(f_x\). If \(x_n = {\texttt{0}}\), we pick the black arrows to map \(2n\) and \(2n+1\), and if \(x_n = 1\) we pick the red/dashed arrows to map \(2n\) and \(2n+1\).
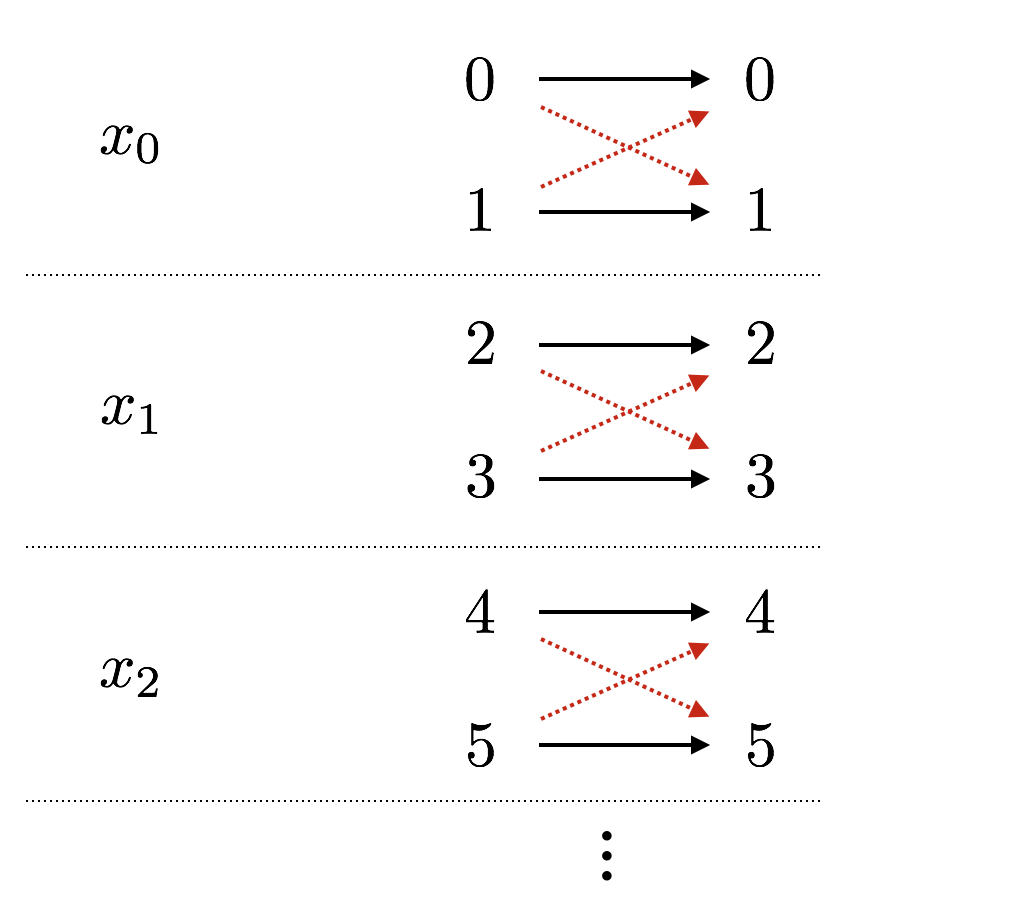
Observe that for any \(x \in \{{\texttt{0}},{\texttt{1}}\}^\infty\), the corresponding function \(f_x\) is indeed a bijection. It is also clear that if \(x \neq x'\), then \(f_{x} \neq f_{x'}\). So this mapping from \(\{{\texttt{0}},{\texttt{1}}\}^\infty\) to \(S\) is indeed an injection. This completes the proof.
Part 2: Let \(S = \{x_1x_2 x_3 \ldots \in \{{\texttt{1}},{\texttt{2}}\}^\infty : \text{ for all $n \geq 1$, $\; \sum_{i=1}^n x_i \not\equiv 0 \mod 4$}\}\). We want to show that \(S\) is uncountable, and we will do so by identifying a subset of \(S\) that is in one-to-one correspondence with \(\{{\texttt{0}},{\texttt{1}}\}^\infty\).
Let \(a = {\texttt{22}}\) and \(b = {\texttt{112}}\). Define the set \(S' = \{{\texttt{1}}w : w \in \{a,b\}^\infty\}\). There are a couple of important observations (whose proofs are omitted):
\(S' \subseteq S\).
The mapping \(f : \{{\texttt{0}},{\texttt{1}}\}^\infty \to \{a,b\}^\infty\) such that \(y_1y_2\ldots \in \{{\texttt{0}},{\texttt{1}}\}^\infty\) is mapped to \(w_1w_2\ldots \in \{a,b\}^\infty\), where \(w_i = a\) if \(y_i = {\texttt{0}}\) and \(w_i = b\) if \(y_i = {\texttt{1}}\), is a bijection.
These two observations imply that we have identified a subset of \(S\) (namely \(S'\)) that is in one-to-one correspondence with \(\{{\texttt{0}},{\texttt{1}}\}^\infty\), which allows us to conclude that \(S\) is uncountable.
For sets \(X, Y\), what are the definitions of \(|X| \leq |Y|\), \(|X| \geq |Y|\), \(|X| = |Y|\), and \(|X| < |Y|\)?
What is the definition of a countable set?
What is the CS method for showing that a set is countable?
True or false: There exists an infinite set \(S\) such that \(|S| < |\mathbb N|\).
True or false: \(\{{\texttt{0}},{\texttt{1}}\}^* \cap \{{\texttt{0}},{\texttt{1}}\}^\infty = \varnothing\).
True or false: \(|\{{\texttt{0}},{\texttt{1}},{\texttt{2}}\}^*| = |\mathbb Q\times \mathbb Q|\).
State the Diagonalization Lemma and briefly explain how it is proved.
What is the connection between Diagonalization Lemma and uncountability?
What is Cantor’s Theorem?
True or false: \(|\wp(\{{\texttt{0}},{\texttt{1}}\}^\infty)| = |\wp(\wp(\{{\texttt{0}},{\texttt{1}}\}^\infty))|\).
True or false: There is a surjection from \(\{{\texttt{0}},{\texttt{1}}\}^\infty\) to \(\{{\texttt{0}},{\texttt{1}},{\texttt{2}},{\texttt{3}}\}^\infty\).
True or false: Let \(\Sigma\) be an alphabet. The set of encodings mapping \(\mathbb N\) to \(\Sigma^*\) is countable.
True or false: Let \(\Sigma = \{{\texttt{1}}\}\) be a unary alphabet. The set of all languages over \(\Sigma\) is countable.
State a technique for proving that a given set is uncountable.
Here are the important things to keep in mind from this chapter.
The definitions of injective, surjective and bijective functions are fundamental.
The concepts of countable and uncountable sets, and their precise mathematical definitions.
When it comes to showing that a set is countable, the CS method is the best choice, almost always.
The Diagonalization Lemma is one of the most important and powerful techniques in all mathematics.
When showing that a set is uncountable, establishing an injection from \(\{0,1\}^\infty\) (or a surjection to \(\{{\texttt{0}},{\texttt{1}}\}^\infty\)) is one of the best techniques you can use.