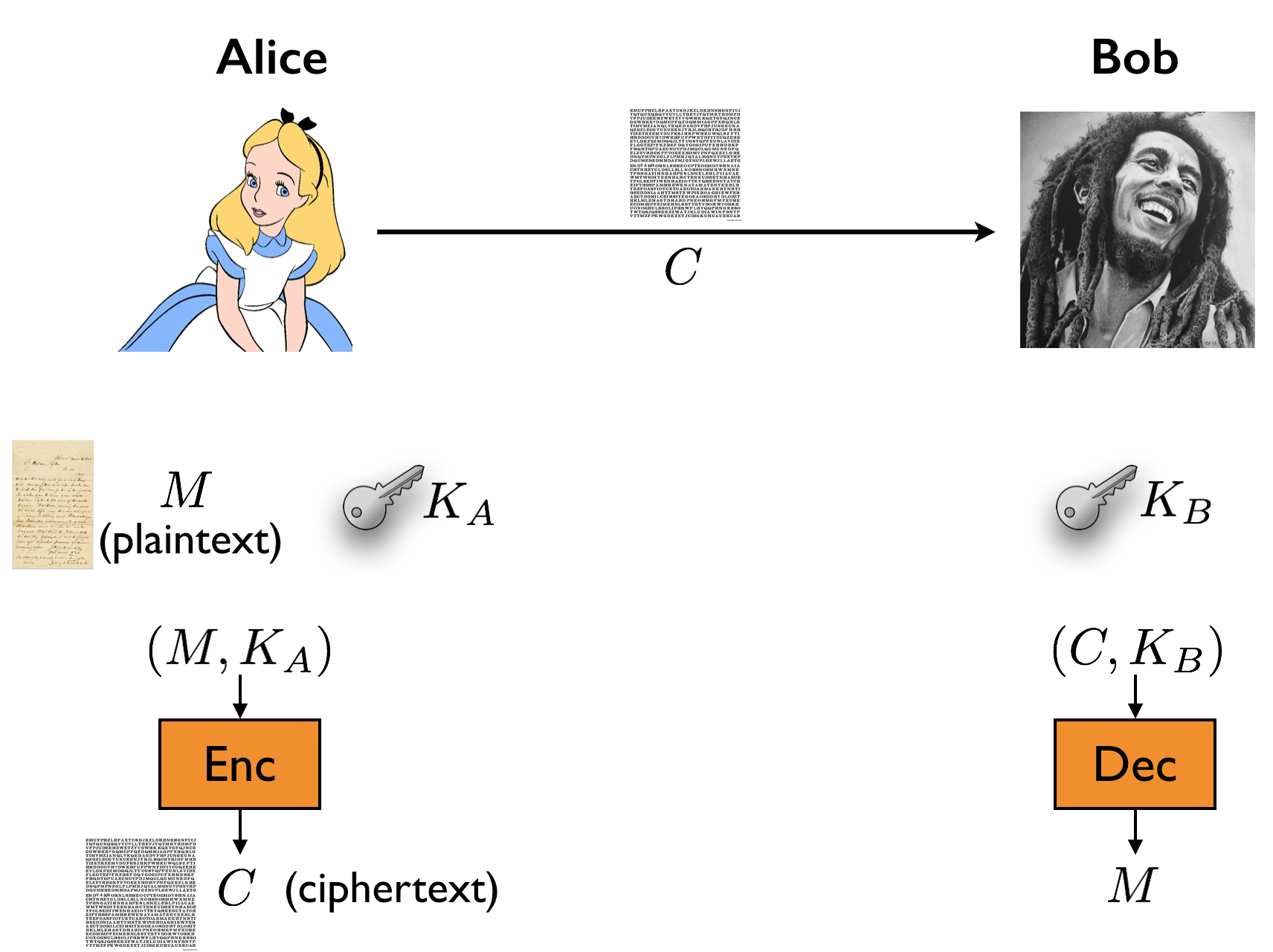
The general setting is as follows. There are three parties named Alice, Bob and Eve. Alice’s goal is to send a private message to Bob over some channel. In particular, Alice wants only Bob to know what her message is, but unfortunately, any message she sends over the channel can be intercepted by the eavesdropper Eve. Therefore, she would like to first encrypt her message (which is also known as the plaintext) and then send the encrypted message (the ciphertext) to Bob over the channel. Bob should be able to decrypt the ciphertext and recover the plaintext. If the system is secure, then Eve learns no information about the plaintext by seeing the ciphertext. If the system is not secure, we will call it broken. We assume that Eve knows the encryption and decryption algorithms used by Alice and Bob respectively.

In a private-key cryptographic system, a protocol is designed as follows. We assume Alice has a private key $K_A$ and Bob has a private key $K_B$. These keys help Alice and Bob encrypt and decrypt messages. In particular, if $M$ is the plaintext that Alice wants to send, she encrypts it using an encryption algorithm $\text{Enc}$ that takes $M$ and $K_A$ as input, and produces a ciphertext $C$ as output: $\text{Enc}(M, K_A) = C$. This ciphertext $C$ is sent to Bob, and Bob uses a decryption algorithm $\text{Dec}$ that takes a ciphertext $C$ and his private key $K_B$ as input, and produces a plaintext $M$: $\text{Dec}(C, K_B) = M$. (We assume that $M, C, K_A, K_B$ are encoded as strings over some finite alphabet $\Sigma$.)

A very simple example of a private-key protocol is the well-known Caesar shift. In this protocol, $0 \leq K_A = K_B \leq 25$ and a plaintext is encrypted by replacing each letter with a letter which is $K_A$ positions down the alphabet. This system is easy to break since the number of possibilities for the key is very small. Therefore one can try each possible key value one by one.

There are much more sophisticated private-key protocols. We now present a simple one that is provably perfectly secure.

In this section, we assume that the plaintext $M \in \{0,1\}^n$ is a binary string of length $n$. Then we choose $K_A = K_B \in \{0,1\}^n$ uniformly at random (and denote it by $K$). The encryption algorithm takes the bit-wise xor of $M$ and $K$ to produce an $n$-bit ciphertext $C$. Or in other words, for each $i$, the $i$’th bit of $C$, $C[i]$, is defined to be $M[i] \oplus K[i]$. Below is an example.

The decryption algorithm is exactly the same as the encryption algorithm. It takes $C$ and $K$ as input, and produces $M$ by taking the bit-wise xor of $C$ and $K$. Observe that for all $i$, $$C[i] \oplus K[i] = (M[i] \oplus K[i]) \oplus K[i] = M[i] \oplus (K[i] \oplus K[i]) = M[i],$$ so the decryption algorithm correctly recovers the original message $M$.

For any plaintext $M \in \{0,1\}^n$, if $K \in \{0,1\}^n$ is chosen uniformly at random, then the ciphertext $C$ is a uniformly random element of $\{0,1\}^n$. This means that Eve learns nothing about $M$ by seeing $C$, so the system is perfectly secure. The downside is that Alice and Bob have to share a key that is as long as the message itself.

It is natural to ask whether there is any perfectly secure system like one-time pad that uses a shorter key. Claude Shannon proved that the answer is “no”. To state his result informally, he showed that if $K$ is shorter than $M$ and Eve is computationally unbounded, then Eve can learn some information about the message $M$.

Given this, we let computational complexity come to our rescue. It is completely reasonable to assume that Eve is indeed computationally bounded. So from now on, we will assume that Eve is a polynomial-time agent.

We present a protocol for Alice and Bob to agree on a secret key $K$ by communicating publicly. The protocol is secure if Eve has no information about $K$ even though she sees all the communication between Alice and Bob. This sounds like an impossible task, but it is actually believed to be feasible.

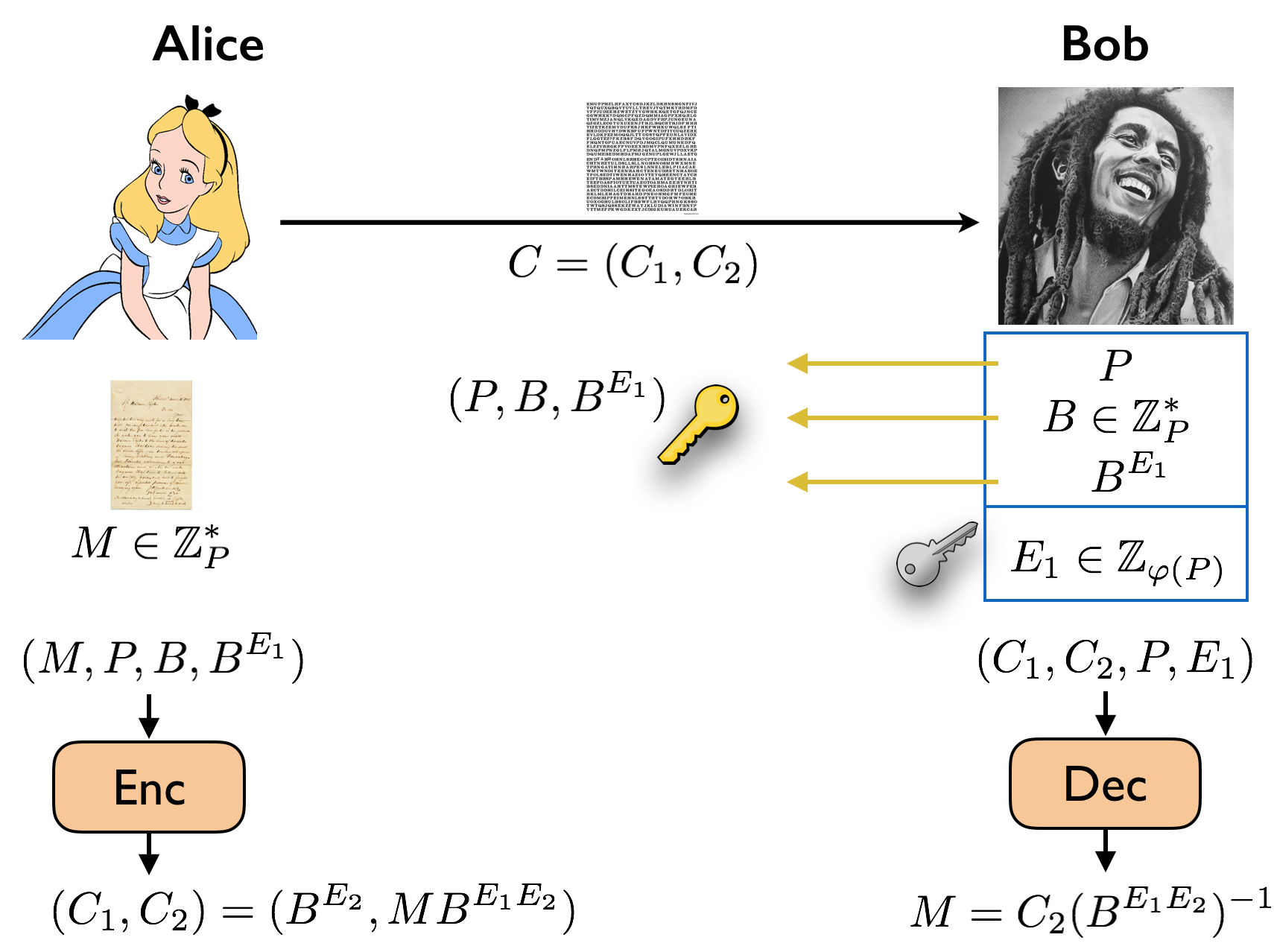
The protocol makes use of the assumption that the Discrete Log problem is computationally hard and it goes as follows. Alice picks privately a (sufficiently large) random prime number $P$, a generator $B$ in $\mathbb Z_P^*$, and a random exponent $E_1 \in \mathbb Z_{\varphi(P)}$. She computes $B^{E_1}$ in $\mathbb Z_P^*$ and sends over to Bob $P, B, B^{E_1}$. Bob privately picks a random exponent $E_2 \in \mathbb Z_{\varphi(P)}$ and computes $B^{E_2}$ in $\mathbb Z_P^*$. He sends $B^{E_2}$ to Alice. At this point both players can privately compute $S = B^{E_1E_2}$ in $\mathbb Z_P^*$, which is defined as the secret key that they now share. The protocol is illustrated below.

There are two important questions related to this protocol. First, are all the operations done by Alice and Bob polynomial-time computable? Second, how secure is the system?

Even though we won’t explicitly discuss it, every computation done by Alice and Bob can indeed be done in polynomial time. For the security, observe that we definitely need the Discrete Log problem to be computationally hard, because otherwise, Eve can compute $E_1$ from $B^{E_1}$ and $E_2$ from $B^{E_2}$. Then it is easy for her to compute the “secret” $B^{E_1E_2}$ (since she also knows $B$). To be more careful though, we want that given $P, B, B^{E_1}, B^{E_2}$ (i.e. what Eve sees), it is computationally hard to compute $B^{E_1E_2}$. This is known as the Diffie-Hellman assumption. Unfortunately we cannot prove this assumption since if we could, we would be also proving $\mathsf{P} \neq \mathsf{NP}$. Even if the Diffie-Hellman assumption holds, we should not be satisfied. Not only we don’t want Eve to compute the secret $B^{E_1E_2}$, but we don’t want her to gain any information about $B^{E_1E_2}$ (e.g. not even the first bit of it). The assumption that Eve learns nothing about the secret is known as the Decisional Diffie-Hellman assumption.

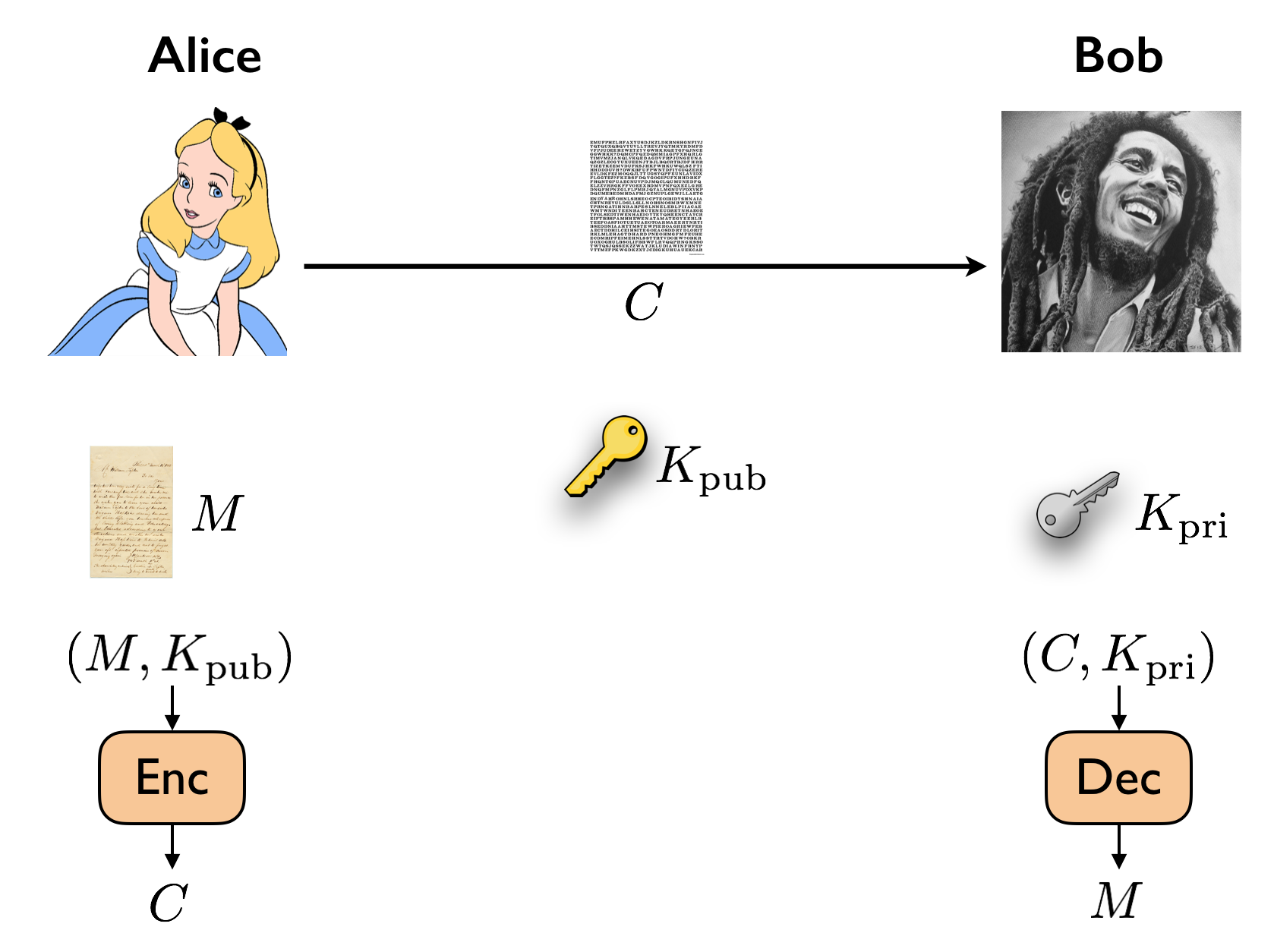
In a public-key cryptographic system, our goal is to design a protocol that allows Alice to send a message to Bob without the need of having to exchange messages in order to share a secret key.

In order to establish this, a public-key cryptographic system uses the following general strategy. Bob generates a tuple of keys $(K_{\text{pri}}, K_{\text{pub}})$, where $K_{\text{pri}}$ is called the private key and is kept private to him, and $K_{\text{pub}}$ is called the public key and is published to the world. If someone (e.g. Alice) wants to send a message to Bob, they use the public key to encrypt their message $M$. That is, the ciphertext $C$ is produced by running an encryption algorithm $\text{Enc}(M, K_{\text{pub}})$. Once Bob receives $C$, he decrypts it using his private key by running a decryption algorithm $\text{Dec}(C, K_{\text{pri}})$.

We now present different instantiations of this idea.

The first public-key protocol we present is similar in nature to the Diffie-Hellman secret-key exchange protocol. In fact, it is basically combining the Diffie-Hellman secret-key exchange protocol with the one-time pad protocol. It is easy to combine them to create a private-key cryptographic system. Here, we’ll see that they can also be combined to create a public-key cryptographic system.

To make the correspondence clear with the Diffie-Hellman secret-key exchange protocol, we reverse the roles of Alice and Bob. Below are the details.

In the ElGamal protcol, Bob picks a (sufficiently large) prime number $P$, a generator $B \in \mathbb Z_P^*$, and a random exponent $E_1 \in \mathbb Z_{\varphi(P)}$. He computes $B^{E_1}$ in $\mathbb Z_P^*$. The private key is $K_{\text{pri}} = E_1$ and the public key is $K_{\text{pub}} = (P, B, B^{E_1})$.

The message $M$ that Alice wants to send is viewed as an element of $\mathbb Z_P^*$ (it is easy to agree on an encoding scheme to do this). To encrypt her message, Alice does the following. She picks a random exponent $E_2 \in \mathbb Z_{\varphi(P)}$, and computes $B^{E_2}$, $B^{E_1E_2}$ and $MB^{E_1E_2}$ in $\mathbb Z_P^*$. Then the ciphertext she sends over to Bob is $C = (C_1, C_2) = (B^{E_2}, MB^{E_1E_2})$. Once Bob receives this message, using $C_1$ he first computes $C_1^{E_1} = B^{E_1E_2}$ in $\mathbb Z_P^*$. Note that this is the secret key from the Diffie-Hellman protocol. Let’s call it $S$. He computes $S^{-1}$ in $\mathbb Z_P^*$. Then he computes $C_2S^{-1} = M$ to recover the original message $M$.

Even though this may seem like a non-simple protocol, it has a simple summary once you understand the Diffie-Hellman secret-key exchange protocol. Effectively, Alice and Bob are sharing the private secret $S = B^{E_1E_2}$ as in the Diffie-Hellman secret-key exchange protocol. Alice “masks” her message $M$ using $S$ (note that this is equivalent to doing a one-time pad in the universe $\mathbb Z_P^*$). Since Bob also knows $S$, he can compute its inverse, and therefore recover $M$.

As in the Diffie-Hellman secret-key exchange protocol, all the computation done by Alice and Bob can be carried out in polynomial time. Furthermore, the security is based on the same assumptions as in the Diffie-Hellman secret-key exchange protocol. The details are omitted.

The RSA cryptographic system uses the assumption that taking roots in the modular universe is a computationally hard problem. Notice that taking roots is the inverse of the exponentiation function. And in RSA, the encryption is indeed done using the exponentiation function. Below are the details.

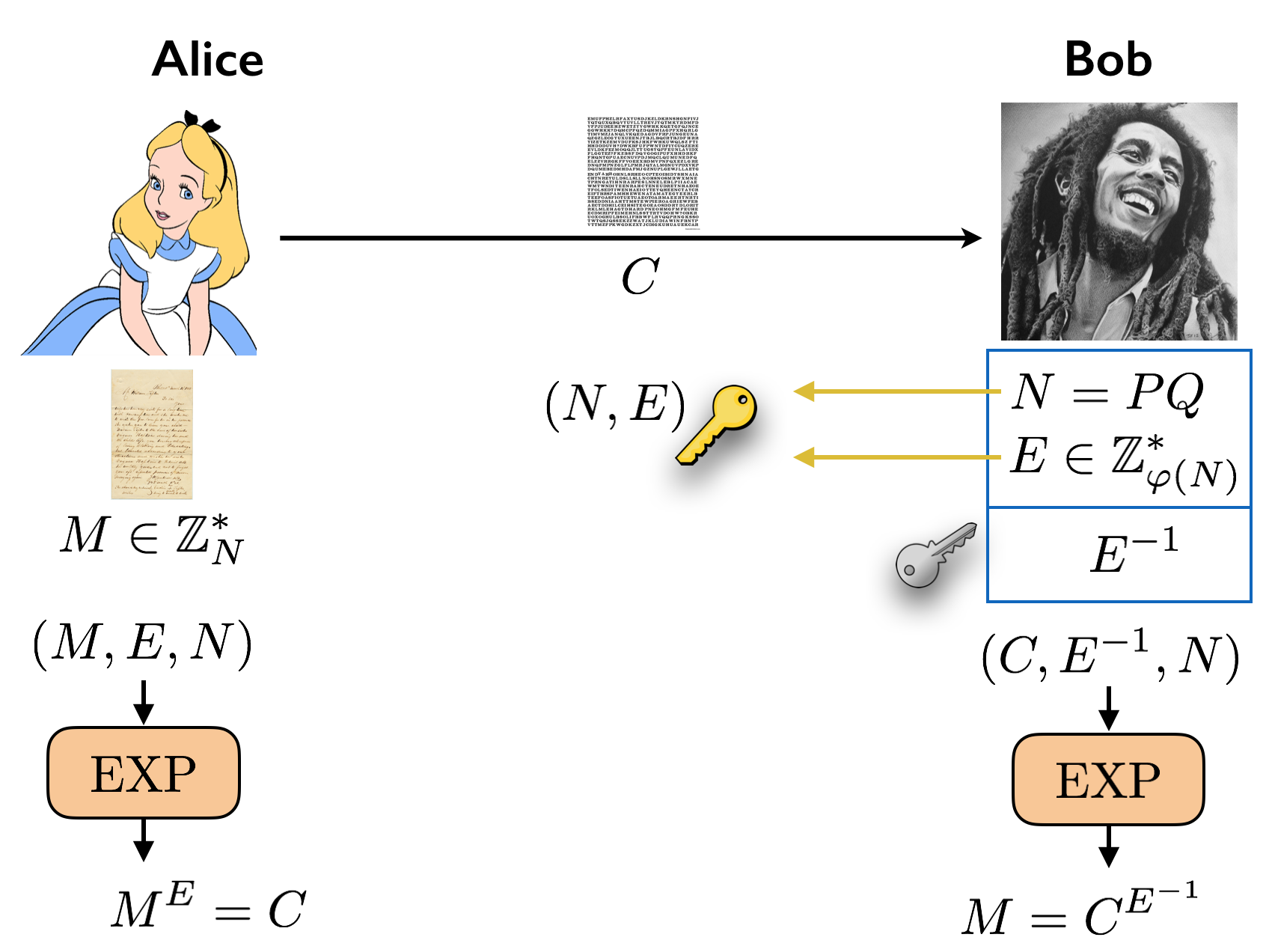
First, Bob picks two (sufficiently large) distinct prime numbers $P$ and $Q$. He multiplies them together to obtain $N = PQ$. He picks an exponent $E \in \mathbb Z_{\varphi(N)}^*$. He computes $E^{-1}$ in $\mathbb Z_{\varphi(N)}^*$ and keeps that as his private key, $K_{\text{pri}} = E^{-1}$. The public key is $K_{\text{pub}} = (N, E)$.

The message $M$ that Alice wants to send to Bob is viewed as an element of $\mathbb Z_N^*$. To encrypt her message, she computes $C = M^E$ in $\mathbb Z_N^*$, and sends it over to Bob. The decryption algorithm happens to be exactly the same as the encryption algorithm. Once Bob receives $C$, he computes $C^{E^{-1}}$ in $\mathbb Z_N^*$, and recovers $M$ since $C^{E^{-1}} = (M^{E})^{E^{-1}} = M^{EE^{-1}} = M$.

As before, it can be shown that all the computation done by Alice and Bob is polynomial-time. We now make a few comments about the security of the system. What is the advantage that Bob has over Eve that allows him to decrypt the message? If Eve could compute $E^{-1}$ herself, then she would be able to decrypt the message as well. To compute $E^{-1}$, you need to know $\varphi(N)$ since $E^{-1}$ lives in $\mathbb Z_{\varphi(N)}^*$. Bob’s advantage is that he can easily compute $\varphi(N)$ because $\varphi(N) = (P-1)(Q-1)$. In other words, the advantage that Bob has is that he knows the prime factorization of $N$. If Eve could factor $N$ efficiently, then she could also easily compute $\varphi(N)= (P-1)(Q-1)$. It turns out that factoring $N$ and computing $\varphi(N)$ are computationally equivalent in the following sense. Clearly, as we argued, if we can factor $N$ in polynomial time, then we can compute $\varphi(N)$ in polynomial time. Furthermore, if we can compute $\varphi(N)$ in polynomial time, then we can factor $N$ in polynomial time (we leave this as an exercise to the reader).

One might ask if computing $\varphi(N)$ is the only way to crack RSA. We don’t know the answer to this question. So we cannot rule out that there might be some other devious way of recovering the message $M$ without computing $\varphi(N)$ (or factoring $N$).