
Our goal in this chapter is to introduce the right language to express and analyze the running time of algorithms, which in return helps us determine which problems are practically decidable, and which problems are (or seem to be) practically undecidable.
Most of the ideas in this chapter will probably be familiar to you at some level as most introductory computer science courses do talk about (asymptotic) running time of algorithms. Nevertheless, it is important to specify some of the details that we will be using as we slowly start approaching the famous \(\mathsf{P}\) vs \(\mathsf{NP}\) question, which is a foundational question about the computational complexity of problems.
For \(f: \mathbb R^+ \to \mathbb R^+\) and \(g: \mathbb R^+ \to \mathbb R^+\), we write \(f(n) = O(g(n))\) if there exist constants \(C > 0\) and \(n_0 > 0\) such that for all \(n \geq n_0\), \[f(n) \leq Cg(n).\] In this case, we say that \(f(n)\) is big-O of \(g(n)\).
Proof 1: To show that \(3n^2 + 10n + 30\) is \(O(n^2)\), we need to show that there exists \(C > 0\) and \(n_0 > 0\) such that \[3n^2 + 10n + 30 \leq Cn^2\] for all \(n \geq n_0\). Pick \(C = 4\) and \(n_0 = 13\). Note that for \(n \geq 13\), we have \[10n + 30 \leq 10n + 3n = 13n \leq n^2.\] This implies that for \(n \geq 13\) and \(C = 4\), \[3n^2 + 10n + 30 \leq 3n^2 + n^2 = Cn^2.\]
Proof 2: Pick \(C = 43\) and \(n_0 = 1\). Then for \(n \geq 1 = n_0\), we have \[3n^2 + 10n + 30 \leq 3n^2 + 10n^2 + 30n^2 = 43n^2 = Cn^2.\]
Using the fact that for all \(m > 0\), \(\log m < m\), show that for all \(\epsilon > 0\) and \(k > 0\), \(\log^k n\) is \(O(n^\epsilon)\).
For this proof, we will use the fact that for all \(m > 0\), \(\log m < m\) with \(m = n^{\epsilon/k}\). So \[\log(n^{\epsilon/k}) < n^{\epsilon/k}.\] Note that \(\log(n^{\epsilon/k}) = \frac{\epsilon}{k} \log n\), and rearranging the terms in the inequality above, we get \[\log n \leq \frac{k}{\epsilon} \cdot n^{\epsilon/k}.\] Taking the \(k\)’th power of both sides gives us, for all \(n > 0\) and \(C = \left(\frac{k}{\epsilon}\right)^k\), \[\log^k n < C n^\epsilon.\]
For \(f: \mathbb R^+ \to \mathbb R^+\) and \(g: \mathbb R^+ \to \mathbb R^+\), we write \(f(n) = \Omega(g(n))\) if there exist constants \(c > 0\) and \(n_0 > 0\) such that for all \(n \geq n_0\), \[f(n) \geq cg(n).\] In this case, we say that \(f(n)\) is big-Omega of \(g(n)\).
To show \((n!)^2 = \Omega(n^n)\), we’ll show that choosing \(c = 1\) and \(n_0=1\) satisfies the definition of Big-Omega. To see this, note that for \(n \geq 1\), we have: \[\begin{aligned} (n!)^2 & = \left((n)(n-1)\cdots (1)\right) \left((n)(n-1) \cdots (1)\right) & \text{(by definition)}\\ & = (n)(1)(n-1)(2) \cdots (1)(n) & \text{(re-ordering terms)}\\ & = ((n)(1))((n-1)(2)) \cdots ((1)(n)) & \text{(pairing up consecutive terms)} \\ & \geq (n)(n) \cdots (n) & \text{(by the Claim below)}\\ & = n^n.\end{aligned}\]
Claim: For \(n \geq 1\) and for \(i \in \{0,1,\ldots,n-1\}\), \[(n-i)(i+1) \geq n.\] Proof: The proof follows from the following chain of implications. \[\begin{aligned} n - (n-1) - 1 = 0 & \quad \implies \quad n-i-1 \geq 0 & \quad \text{(since $i \leq n-1$)} \\ & \quad \implies \quad i(n-i-1) \geq 0 & \quad \text{(since $i \geq 0$)} \\ & \quad \implies \quad ni - i^2 - i \geq 0 & \\ & \quad \implies \quad ni - i^2 - i + n \geq n & \\ & \quad \implies \quad (n-i)(i+1) \geq n. &\end{aligned}\] This completes the proof.
For \(f: \mathbb R^+ \to \mathbb R^+\) and \(g: \mathbb R^+ \to \mathbb R^+\), we write \(f(n) = \Theta(g(n))\) if \[f(n) = O(g(n)) \quad \quad \text{and} \quad \quad f(n) = \Omega(g(n)).\] This is equivalent to saying that there exists constants \(c,C,n_0 > 0\) such that for all \(n \geq n_0\), \[cg(n) \leq f(n) \leq Cg(n).\] In this case, we say that \(f(n)\) is Theta of \(g(n)\).
For any constant \(b > 1\), \[\log_b n = \Theta(\log n).\]
It is well known that \(\log_b n = \frac{\log_a n}{\log_a b}\). In particular \(\log_b n = \frac{\log_2 n}{\log_2 b}\). Then taking \(c = C = \frac{1}{\log_2 b}\) and \(n_0 = 1\), we see that \(c \log_2 n \leq \log_b n \leq C \log_2 n\) for all \(n \geq n_0\). Therefore \(\log_b n = \Theta(\log_2 n)\).
Since the base of a logarithm only changes the value of the log function by a constant factor, it is usually not relevant in big-O, big-Omega or Theta notation. So most of the time, when you see a \(\log\) function present inside \(O(\cdot)\), \(\Omega(\cdot)\), or \(\Theta(\cdot)\), the base will be ignored. E.g. instead of writing \(\ln n = \Theta(\log_2 n)\), we actually write \(\ln n = \Theta(\log n)\). That being said, if the \(\log\) appears in the exponent, the base matters. For example, \(n^{\log_2 5}\) is asymptotically different from \(n^{\log_3 5}\).
We first show \(\log_2 n! = O(n \log n)\). Observe that \[n! \quad = \quad n \cdot (n-1) \cdot (n-2) \cdot \cdots \cdot 2 \cdot 1 \quad \leq \quad \underbrace{n \cdot n \cdot n \cdot \cdots \cdot n}_{n \text{ times}} \quad = \quad n^n,\] as each term on the RHS (i.e. \(n\)) is greater than or equal to each term on the LHS. Taking the \(\log\) of both sides gives us \(\log_2 n! \leq \log_2 n^n = n \log_2 n\) (here, we are using the fact that \(\log a^b = b \log a\)). Therefore taking \(n_0 = C = 1\) satisfies the definition of big-O, and \(\log_2 n! = O(n \log n)\).
Now we show \(\log_2 n! = \Omega(n \log n)\). Assume without loss of generality that \(n\) is even. In the definition of \(n!\), we’ll use the first \(n/2\) terms in the product to lower bound it: \[n! \quad = \quad n \cdot (n-1) \cdot (n-2) \cdot \cdots \cdot 2 \cdot 1 \quad \geq \quad \underbrace{\frac{n}{2} \cdot \frac{n}{2} \cdot \cdots \cdot \frac{n}{2}}_{n/2 \text{ times} } \quad = \quad \left(\frac{n}{2}\right)^{\frac{n}{2}}.\] Taking the \(\log\) of both sides gives us \(\log_2 n! \geq \frac{n}{2} \log_2 \frac{n}{2}\).
Claim: For \(n \geq 4\), \(\frac{n}{2} \log_2 \frac{n}{2} \geq \frac{n}{4} \log_2 n\).
The proof of the claim is not difficult (some algebraic manipulation) and is left for the reader. Using the claim, we know that for \(n \geq 4\), \(\log_2 n! \geq \frac{n}{4} \log_2 n\). Therefore, taking \(n_0 = 4\) and \(c = 1/4\) satisfies the definition of big-Omega, and \(\log_2 n! = \Omega(n \log n)\).
Suppose we are using some computational model in which what constitutes a step in an algorithm is understood. Suppose also that for any input \(x\), we have an explicit definition of its length. The worst-case running time of an algorithm \(A\) is a function \(T_A : \mathbb N\to \mathbb N\) defined by \[T_A(n) = \max_{\substack{\text{instances/inputs $x$} \\ \text{of length $n$}}} \text{ number of steps $A$ takes on input $x$}.\] We drop the subscript \(A\) and just write \(T(n)\) when \(A\) is clear from the context.
We use \(n\) to denote the input length. Unless specified otherwise, \(n\) is defined to be the number of bits in a reasonable binary encoding of the input. It is also common to define \(n\) in other ways. For example, if the input is an array or a list, \(n\) can denote the number of elements.
In the Turing machine model, a step in the computation corresponds to one application of the transition function of the machine. However, when measuring running time, often we will not be considering the Turing machine model.
If we don’t specify a particular computational model, by default, our model will be closely related to the Random Access Machine (RAM) model. Compared to TMs, this model aligns better with the architecture of the computers we use today. We will not define this model formally, but instead point out two properties of importance.
First, given a string or an array, accessing any index counts as 1 step.
Second, arithmetic operations count as 1 step as long as the numbers involved are “small”. We say that a number \(y\) is small if it can be upper bounded by a polynomial in \(n\), the input length. That is, \(y\) is small if there is some constant \(k\) such that \(y\) is \(O(n^k)\). As an example, suppose we have an algorithm \(A\) that contains a line like \(x = y + z\), where \(y\) and \(z\) are variables that hold integer values. Then we can count this line as a single step if \(y\) and \(z\) are both small. Note that whether a number is small or not is determined by the length of the input to the algorithm \(A\).
We say that a number is large, if it is not small, i.e., if it cannot be upper bounded by a polynomial in \(n\). In cases where we are doing arithmetic operations involving large numbers, we have to consider the algorithms used for the arithmetic operations and figure out their running time. For example, in the line \(x = y + z\), if \(y\) or \(z\) is a large number, we need to specify what algorithm is being used to do the addition and what its running time is. A large number should be treated as a string of digits/characters. Arithmetic operations on large numbers should be treated as string manipulation operations and their running time should be figured out accordingly.
The expression of the running time of an algorithm using big-O, big-Omega or Theta notation is referred to as asymptotic complexity estimate of the algorithm.
\[\begin{aligned} \text{Constant time:} & \quad T(n) = O(1). \\ \text{Logarithmic time:} & \quad T(n) = O(\log n). \\ \text{Linear time:} & \quad T(n) = O(n). \\ \text{Quadratic time:} & \quad T(n) = O(n^2). \\ \text{Polynomial time:} & \quad T(n) = O(n^k) \text{ for some constant $k > 0$}. \\ \text{Exponential time:} & \quad T(n) = O(2^{n^k}) \text{ for some constant $k > 0$}.\end{aligned}\]
We denote by \(\mathsf{P}\) the set of all languages that can be decided in polynomial-time, i.e., in time \(O(n^k)\) for some constant \(k>0\).
Suppose that we have an algorithm \(A\) that runs another algorithm \(A'\) once as a subroutine. We know that the running time of \(A'\) is \(O(n^k)\), \(k \geq 1\), and the work done by \(A\) is \(O(n^t)\), \(t \geq 1\), if we ignore the subroutine \(A'\) (i.e., we don’t count the steps taken by \(A'\)). What kind of upper bound can we give for the total running-time of \(A\) (which includes the work done by \(A'\))?
Let \(n\) be the length of the input to algorithm \(A\). The total work done by \(A\) is \(f(n) + g(n)\), where \(g(n)\) is the work done by the subroutine \(A'\) and \(f(n) = O(n^t)\) is the work done ignoring the subroutine \(A'\).
We analyze \(g(n)\) as follows. Note that in time \(O(n^t)\), \(A\) can produce a string of length \(cn^t\) (for some constant \(c\)), and feed this string to \(A'\). The running time of \(A'\) is \(O(m^k)\), where \(m\) is the length of the input for \(A'\). When \(A\) is run and calls \(A'\), the length of the input to \(A'\) can be \(m = cn^t\). Therefore, the work done by \(A'\) inside \(A\) is \(O(m^k) = O((cn^t)^k) = O(c^k n^{tk}) = O(n^{tk})\).
Since \(f(n) = O(n^t)\) and \(g(n) = O(n^{tk})\), we have \(f(n) + g(n) = O(n^{tk})\).
The intrinsic complexity of \(L = \{0^k1^k : k \in \mathbb N\}\) is \(\Theta(n)\).
We want to show that the intrinsic complexity of \(L = \{0^k1^k : k \in \mathbb N\}\) is \(\Theta(n)\). The proof has two parts. First, we need to argue that the intrinsic complexity is \(O(n)\). Then, we need to argue that the intrinsic complexity is \(\Omega(n)\).
To show that \(L\) has intrinsic complexity \(O(n)\), all we need to do is present an algorithm that decides \(L\) in time \(O(n)\). We leave this as an exercise to the reader.
To show that \(L\) has intrinsic complexity \(\Omega(n)\), we show that no matter what algorithm is used to decide \(L\), the number of steps it takes must be at least \(n\). We prove this by contradiction, so assume that there is some algorithm \(A\) that decides \(L\) using \(n-1\) steps or less. Consider the input \(x = 0^k1^k\) (where \(n = 2k\)). Since \(A\) uses at most \(n-1\) steps, there is at least one index \(j\) with the property that \(A\) does not access \(x[j]\). Let \(x'\) be the input that is the same as \(x\), except the \(j\)’th coordinate is reversed. Since \(A\) does not access the \(j\)’th coordinate, it has no way of distinguishing between \(x\) and \(x'\). In other words, \(A\) behaves exactly the same when the input is \(x\) or \(x'\). But this contradicts the assumption that \(A\) correctly decides \(L\) because \(A\) should accept \(x\) and reject \(x'\).
In the TM model, a step corresponds to one application of the transition function. Show that \(L = \{0^k1^k : k \in \mathbb N\}\) can be decided by a TM in time \(O(n \log n)\). Is this statement directly implied by Proposition (Intrinsic complexity of \(\{0^k1^k : k \in \mathbb N\}\))?
First of all, the statement is not directly implied by Proposition (Intrinsic complexity of \(\{0^k1^k : k \in \mathbb N\}\)) because that proposition is about the RAM model whereas this question is about the TM model.
We now sketch the solution. Below is a medium-level description of a TM deciding the language \(\{0^k1^k : k \in \mathbb N\}\).
Scan the tape.
If there is a 0 symbol after a 1 symbol, reject.
Repeat while both 0s and 1s remain on the tape:
Scan the tape.
If (number of 1s + number of 0s) is odd, reject.
Scan the tape.
Cross off every other 0 starting with first 0.
Cross off every other 1 starting with first 1.
If no 0s and no 1s remain accept.
Else, reject. Let \(n\) be the input length. Observe that in each iteration of the loop, we do \(O(n)\) work, and the number of iterations is \(O(\log n)\) because in each iteration, half of the non-crossed portion of the input gets crossed off (i.e. in each iteration, the number of \(0\)’s and \(1\)’s is halved). So the total running time is \(O(n \log n)\).
Assume the languages \(L_1\) and \(L_2\) are decidable in polynomial time. Prove or give a counter-example: \(L_1L_2\) is decidable in polynomial time.
Let \(M_1\) be a decider for \(L_1\) with running-time \(O(n^k)\) and let \(M_2\) be a decider for \(L_2\) with running-time \(O(n^t)\). We construct a polynomial-time decider for \(L_1L_2\) as follows:
\[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; M(x):\\ &{\scriptstyle 1.}~~~~\texttt{For each of the $|x| + 1$ ways to divide $x$ as $yz$:}\\ &{\scriptstyle 2.}~~~~~~~~\texttt{Run $M_1(y)$.}\\ &{\scriptstyle 3.}~~~~~~~~\texttt{If it accepts:}\\ &{\scriptstyle 4.}~~~~~~~~~~~~\texttt{Run $M_2(z)$.}\\ &{\scriptstyle 5.}~~~~~~~~~~~~\texttt{If it accepts, accept.}\\ &{\scriptstyle 6.}~~~~\texttt{Reject.}\\ \hline\hline\end{aligned}\]
The input length is \(n = |x|\). The for-loop repeats \(n+1\) times. In each iteration of the loop, we do at most \(cn^k + c'n^t + c''\) work, where \(c, c', c''\) are constants independent of \(n\). So the total running-time is \(O(n^{\max\{k,t\}+1})\).
Given a computational problem with an integer input \(x\), notice that \(x\) is a large number (if \(x\) is \(n\) bits long, its value can be about \(2^n\), so it cannot be upper bounded by a polynomial in \(n\)). Therefore arithmetic operations involving \(x\) cannot be treated as 1-step operations. Computational problems with integer input(s) are the most common examples in which we have to deal with large numbers, and in these situations, one should be particularly careful about analyzing running time.
In the integer addition problem, we are given two \(n\)-bit numbers \(x\) and \(y\), and the output is their sum \(x+y\). In the integer multiplication problem, we are given two \(n\)-bit numbers \(x\) and \(y\), and the output is their product \(xy\).
Consider the following algorithm for the integer addition problem (we’ll assume the inputs are natural numbers for simplicity).
\[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; \text{Addition}(\langle \text{natural } x,\; \text{natural } y \rangle):\\ &{\scriptstyle 1.}~~~~\texttt{For $i = 1$ to $x$:}\\ &{\scriptstyle 2.}~~~~~~~~\texttt{$y = y + 1$.}\\ &{\scriptstyle 3.}~~~~\texttt{Return $y$.}\\ \hline\hline\end{aligned}\]
This algorithm has a loop that repeats \(x\) many times. Since \(x\) is an \(n\)-bit number, the worst-case complexity of this algorithm is \(\Omega(2^n)\).
In comparison, the following well-known algorithm for integer addition has time complexity \(O(n)\).
\[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; \text{Addition}(\langle \text{natural } x,\; \text{natural } y \rangle):\\ &{\scriptstyle 1.}~~~~\text{carry} = 0.\\ &{\scriptstyle 2.}~~~~\texttt{For $i = 0$ to $n-1$:}\\ &{\scriptstyle 3.}~~~~~~~~\text{columnSum} = x[i] + y[i] + \text{carry}.\\ &{\scriptstyle 4.}~~~~~~~~z[i] = \text{columnSum} \; \% \;2.\\ &{\scriptstyle 5.}~~~~~~~~\text{carry} = (\text{columnSum} - z[i])/2.\\ &{\scriptstyle 6.}~~~~z[n] = \text{carry}.\\ &{\scriptstyle 7.}~~~~\texttt{Return $z$.}\\ \hline\hline\end{aligned}\]
Note that the arithmetic operations inside the loop are all \(O(1)\) time since the numbers involved are all bounded (i.e., their values do not depend on \(n\)). Since the loop repeats \(n\) times, the overall complexity is \(O(n)\).
It is easy to see that the intrinsic complexity of integer addition is \(\Omega(n)\) since it takes at least \(n\) steps to write down the output, which is either \(n\) or \(n+1\) bits long. Therefore we can conclude that the intrinsic complexity of integer addition is \(\Theta(n)\). The same is true for integer subtraction.
Consider the following problem: Given as input a positive integer \(N\), output a non-trivial factor of \(N\) if one exists, and output False otherwise. Give a lower bound using the \(\Omega(\cdot)\) notation for the running-time of the following algorithm solving the problem:
\[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; \text{Non-Trivial-Factor}(\langle \text{natural } N \rangle):\\ &{\scriptstyle 1.}~~~~\texttt{For $i = 2$ to $N-1$:}\\ &{\scriptstyle 2.}~~~~~~~~\texttt{If $N \;\%\; i == 0$: Return $i$.}\\ &{\scriptstyle 3.}~~~~\texttt{Return False.}\\ \hline\hline\end{aligned}\]
The input is a number \(N\), so the length of the input is \(n\), which is about \(\log_2 N\). In other words, \(N\) is about \(2^n\). In the worst-case, \(N\) is a prime number, which would force the algorithm to repeat \(N-2\) times. Therefore the running-time of the algorithm is \(\Omega(N)\). Writing \(N\) in terms of \(n\), the input length, we get that the running-time is \(\Omega(2^n)\).
The grade-school algorithms for the integer multiplication and division problems have time complexity \(O(n^2)\).
The integer multiplication problem can be solved in time \(O(n^{1.59})\).
Our goal is to present an algorithm with running time \(O(n^{1.59})\) that solves the integer multiplication problem where the input is two \(n\)-bit numbers \(x\) and \(y\). For simplicity, we assume that \(n\) is a power of 2. The argument can be adapted to handle other values of \(n\). We first present the algorithm (which is recursive), and then put an upper bound on its running time complexity.
Let \(x\) and \(y\) be the input integers, each \(n\) bits long. Observe that we can write \(x\) as \(a \cdot 2^{n/2} + b\), where \(a\) is the number corresponding to the left \(n/2\) bits of \(x\) and \(b\) is the number corresponding to the right \(n/2\) bits of \(x\). For example, if \(x = 1011\) then \(a = 10\) and \(b = 11\). We can similarly write \(y\) as \(c \cdot 2^{n/2} + d\). Then the product of \(x\) and \(y\) can be written as: \[\begin{aligned} x \cdot y & = (a \cdot 2^{n/2} + b)(c \cdot 2^{n/2} + d) \\ & = ac \cdot 2^n + (ad + bc) \cdot 2^{n/2} + bd\end{aligned}\] This implies that we can compute \(xy\) by recursively computing the products \(ac\), \(ad\), \(bc\) and \(bd\). Note that multiplying a number by \(2^n\) is just putting \(n\) 0’s at the end of the number, so this has cost \(O(n)\). Similarly all the addition operations are \(O(n)\) time.
Our algorithm is slightly different than the one described above. We will do the calculation with only 3 recursive calls rather than 4. We recursively compute the products \(ac\), \(bd\) and \((a-b)(c-d)\). Observe that \((a - b)(c - d) - ac - bd = -(ad + bc)\). Now that we have \(ac\), \(bd\) and \((ad + bc)\) at hand, we can compute \(xy\) (of course we still have to do the appropriate addition operations and padding with \(0\)’s). This completes the description of the algorithm.
Let \(T(n)\) be the time complexity of our algorithm. Observe that the recursive relation that \(T(n)\) satisfies is \[T(1) = k, \quad \quad T(n) \leq 3T(n/2) + cn \quad \text{for $n > 1$},\] where \(k\) and \(c\) are some constants. The base case corresponds to 1-bit integers, which can be calculated in constant time. In \(T(n) \leq 3T(n/2) + cn\), the \(3T(n/2)\) comes from the 3 recursive calls we make to compute the products \(ac\), \(bd\) and \((a-b)(c-d)\). The \(cn\) comes from the work we have to do for the addition operations and the padding with 0’s. To solve the recursion, i.e., to figure out the formula for \(T(n)\), we draw the associated recursion tree.
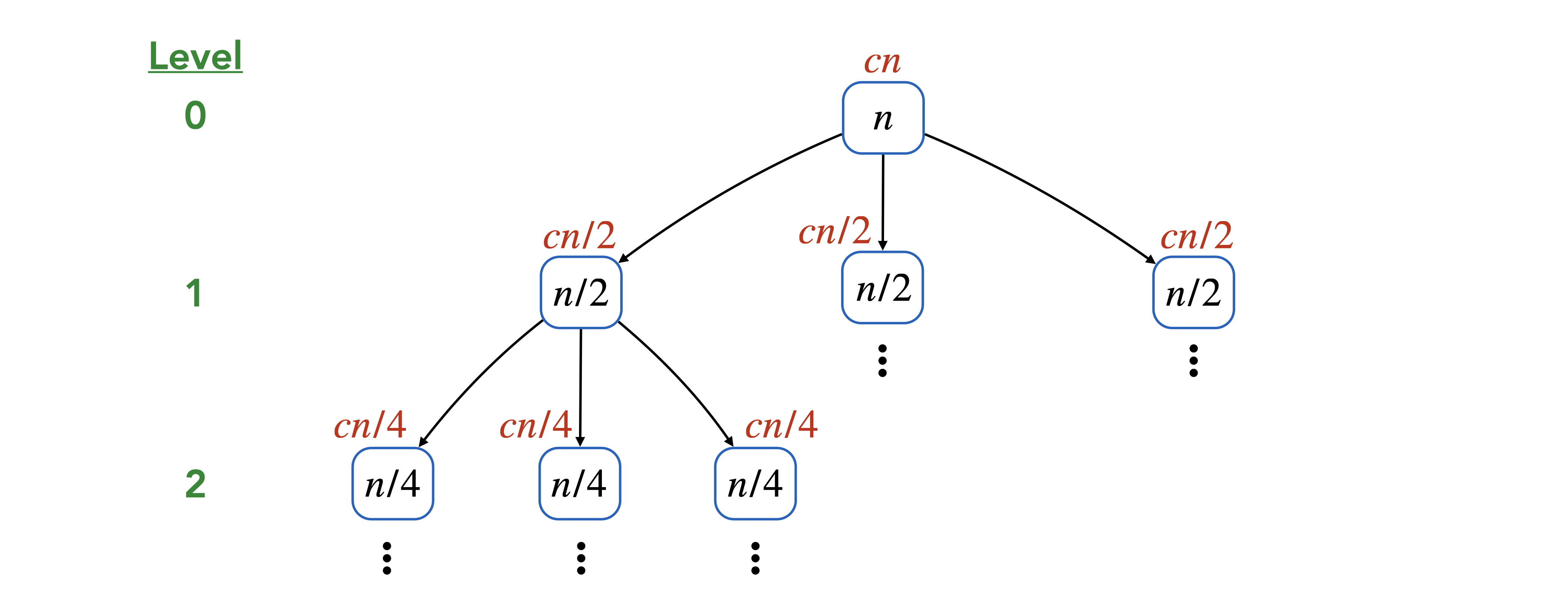
The root (top) of the tree corresponds to the original input with \(n\)-digit numbers and is therefore labeled with an \(n\). This branches off into 3 nodes, one corresponding to each recursive call. These nodes are labeled with \(n/2\) since they correspond to recursive calls in which the number of bits is halved. Those nodes further branch off into 3 nodes, and so on, until at the very bottom, we end up with nodes corresponding to inputs with \(n = 1\). The work being done for each node of the tree is provided with a label on top of the node. For example, at the root (top), we do at most \(cn\) work before we do our recursive calls. This is why we put a \(cn\) on top of that node. Similarly, every other node can be labeled, and the total work done by the algorithm is the sum of all the labels.
We now calculate the total work done. We can divide the nodes of the tree into levels according to how far a node is from the root. So the root corresponds to level 0, the nodes it branches off to correspond to level 1, and so on. Observe that level \(j\) has exactly \(3^j\) nodes. The nodes that are at level \(j\) each do \(cn/2^j\) work. Therefore, the total work done at level \(j\) is \(cn3^j/2^j\). The last level corresponds to level \(\log_2 n\). Thus, we have: \[T(n) \leq \sum_{j = 0}^{\log_2 n} cn (3^j/2^j) = cn \sum_{j=0}^{\log_2 n} (3^j/2^j)\] Using the formula for geometric sums, we can say that there is some constant \(C\) such that: \[T(n) \leq Cn (3^{\log_2 n} / 2^{\log_2 n}) = Cn (n^{\log_2 3} / n^{\log_2 2}) = C n^{\log_2 3}.\] So we conclude that \(T(n) = O(n^{1.59})\).
The programming language Python uses Karatsuba algorithm for multiplying large numbers. There are algorithms for multiplying integers that are asymptotically better than the Karatsuba algorithm.
Consider the following computational problem. Given as input a number \(A \in \mathbb{N}\), output \(\lfloor A^{1/251}\rfloor\). Determine whether this problem can be computed in worst-case polynomial-time, i.e. \(O(n^k)\) time for some constant \(k\), where \(n\) denotes the number of bits in the binary representation of the input \(A\). If you think the problem can be solved in polynomial time, give an algorithm in pseudocode, explain briefly why it gives the correct answer, and argue carefully why the running time is polynomial. If you think the problem cannot be solved in polynomial time, then provide a proof.
First note that the following algorithm, although correct, is exponential time.
\[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; \text{Linear-Search}(\langle \text{natural } A \rangle):\\ &{\scriptstyle 1.}~~~~\texttt{For $B = 0$ to $A$:}\\ &{\scriptstyle 2.}~~~~~~~~\texttt{If $B^{251} > A$: Return $B-1$.}\\ \hline\hline\end{aligned}\]
The length of the input is \(n\), which is about \(\log_2 A\). In other words, \(A\) is about \(2^n\). The for loop above will repeat \(\lfloor A^{1/251} \rfloor\) many times, so the running-time is \(\Omega(A^{1/251})\), and in terms of \(n\), this is \(\Omega(2^{n/251})\).
To turn the above idea into a polynomial-time algorithm, we need to use binary search instead of linear search.
\[\begin{aligned} \hline\hline\\[-12pt] &\textbf{def}\;\; \text{Binary-Search}(\langle \text{natural } A \rangle):\\ &{\scriptstyle 1.}~~~~\text{lo} = 0.\\ &{\scriptstyle 2.}~~~~\text{hi} = A.\\ &{\scriptstyle 3.}~~~~\texttt{While }(\text{lo} < \text{hi}):\\ &{\scriptstyle 4.}~~~~~~~~B = \left\lceil \frac{\text{lo} + \text{hi}}{2} \right\rceil.\\ &{\scriptstyle 5.}~~~~~~~~\texttt{If } B^{251} > A \texttt{: } \text{hi} = B-1.\\ &{\scriptstyle 6.}~~~~~~~~\texttt{Else: } \text{lo} = B.\\ &{\scriptstyle 7.}~~~~\texttt{Return } \text{lo}.\\ \hline\hline\end{aligned}\]
Since we are using binary search, we know that the loop repeats \(O(\log A)\) times, or using \(n\) as our parameter, \(O(n)\) times. All the variables hold values that are at most \(A\), so they are at most \(n\)-bits long. This means all the arithmetic operations (plus, minus, and division by 2) in the loop can be done in linear time. Computing \(B^{251}\) is polynomial-time because we can compute it by doing integer multiplication a constant number of times, and the numbers involved in these multiplications are \(O(n)\)-bits long. Thus, the total work done is polynomial in \(n\).
What is the formal definition of “\(f = \Omega(g)\)”?
True or false: \(n^{\log_2 5} = \Theta(n^{\log_3 5})\).
True or false: \(n^{\log_2 n} = \Omega(n^{15251})\).
True or false: \(3^n = \Theta(2^n)\).
True or false: Suppose \(f(n) = \Theta(g(n))\). Then we can find constants \(c > 0\) and \(n_0 > 0\) such that for all \(n \geq n_0\), \(f(n) = cg(n)\).
True or false: \(f(n) = O(g(n))\) if and only if \(g(n) = \Omega(f(n))\).
What is the definition of “worst-case running time of an algorithm \(A\)”?
True or false: Let \(\Sigma = \{{\texttt{0}},{\texttt{1}}\}\) and let \(L = \{{\texttt{0}}^n : n \in \mathbb{N}^+\}\). There is a Turing machine \(A\) deciding \(L\) whose running time \(T_A\) satisfies “\(T_A(n)\) is \(O(n)\)”.
True or false: Continuing previous question, every Turing machine \(B\) that decides \(L\) has running time \(T_B\) satisfying “\(T_B(n)\) is \(\Omega(n)\)”.
True or false: The intrinsic complexity of the integer multiplication problem is \(\Theta(n^{\log_2 3})\).
True or false: For languages \(L_1\) and \(L_2\), if \(L_1 \leq L_2\) and \(L_2\) is polynomial time decidable, then \(L_1\) is polynomial time decidable.
Explain under what circumstances we count arithmetic operations as constant-time operations, and under what circumstances we don’t.
Consider the algorithm below. What is \(n\), the input length? Is the algorithm polynomial time?
def isPrime(N): if (N < 2): return False if (N == 2): return True if (N mod 2 == 0): return False maxFactor = ceiling(N**0.5) # N**0.5 = square root of N for factor in range(3,maxFactor+1,2): if (N mod factor == 0): return False return True
Here are the important things to keep in mind from this chapter.
Both an intuitive and formal understanding of big-O, big-Omega and Theta notations are important.
The definition of “Worst-case running time of an algorithm” is fundamental.
Understanding how to analyze the running time of algorithms that involve integer inputs is one of the main goals of this chapter. The key here is to always keep in mind that if an algorithm has an integer \(N\) as input, the input length \(n\) is not \(N\), but rather the logarithm of \(N\). If you are not careful about this, you can fool yourself into thinking that exponential time algorithms are actually polynomial time algorithms.
Make sure you understand when arithmetic operations count as constant time operations and when they do not.
You should be comfortable solving recurrence relations using the tree method, as illustrated in the proof of Theorem (Karatsuba algorithm for integer multiplication).